空間相転移が起きたところで
東京大学2015年度理系第二問の確率の問題の解説をしたいと思います。
[問題]

どの目も出る確率が1/6のさいころを1つ用意し、次のように左から順に文字を書く。
さいころを投げ、出た芽が1,2,3のときは文字列AAを書き、4のときは文字Bを、5のときは文字Cを、6のときは文字Dを書く。さらに繰り返しさいころを投げ、同じ規則に従って、AA,B,C,Dをすでにある文字列の右側につなげて書いていく。
たとえばさいころを5回投げ、その出た目が順に2,5,6,3,4であったとすると、得られる文字列は
AACDAAB
となる。このとき、左から4番目の文字はD,5番目の文字はAである。
(1)nを正の整数とする。n回さいころを投げ文字列を作るとき、文字列の左からn番目の文字がAとなる確率を求めよ。
(2)nを2以上の整数とする。n回さいころを投げ、文字列を作るとき、文字列の左からn-1番目の文字がAで、かつn番目の文字がBとなる確率を求めよ。
[解答と解説]]
(1)
そうやな、まずはBかCかDの文字をXとか書いておくねん。
よっしゃよっしゃ
これでなAAが来ると文字数が増えるからな。。
何個AA出るかで場合分けするねん。
AAが1個のときは
XX…XAAで(1/2)^(n-2)・1/2
XX…XXAAで(1/2)^(n-1)・1/2
AAが2個のときは
AAXX…XAAで(n-3)_C1・(1/2)^(n-3)・1/2
AAXX…XXAAで(n-2)_C1・(1/2)^(n-2)・1/2
AAが3個のときは
AAAAX…XAA…(n-4)_C_2・(1/2)^(n-4)・1/2
AAAAX…XXAA…(n-3)_C_2・(1/2)^(n-3)・1/2
ちゃうねん、ちゃうねん。
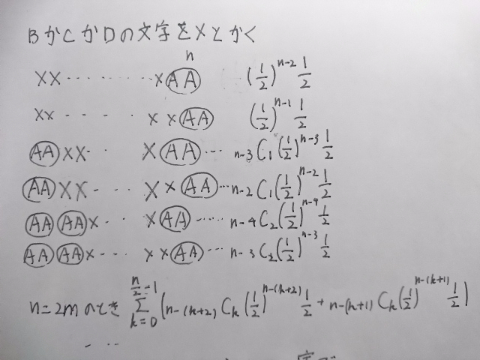
これでΣ計算するねん
n=2mのとき
Σ(k=0~(n/2-1))((n-(k+2))_C_k・(1/2)^(n-(k+2))1/2+(n-(k+1))_C_k(1/2)^(n-(k+1))1/2)
…
ってやってると
マンションの1室で撮影会がおこなれることになります。
こんなことになると、自分の撮影が回ってきたときに
無言で撮ってたら
何も話さないよね?って
当たり前のようにみんな一眼レフを持ってきてポーズの指示出して撮ってそんなこと言われてもってなります。
そこで最初に言ったように空間相転移を起こして
n回さいころを振って出来た並びの事象に分けるんじゃなくて
n番目の文字が何であるのか事象に分けて考えてみるねん。
準備として
1,2,3の目が出たときの文字列をA_LA_RってAはAでも左のAか右のAかに分けよか。
4,5,6の目が出たときの文字列をXとかくとしよか。
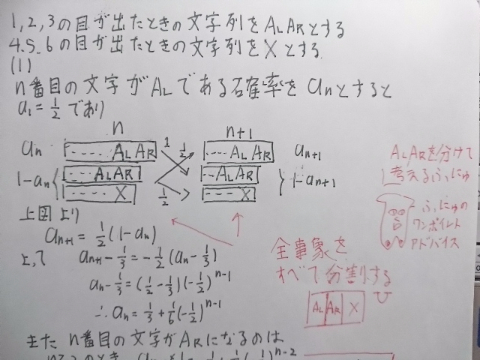
n番目の文字がA_Lである確率をa_nとすると
まずa_1=1/2やろ。
それで漸化式を立てるねんけどコツは
n番目とn+1番目で全事象を分けるねん。
分け方はさっき書いたように
n番目の文字が何かを基準に事象を分けるねん。
n番目の文字はA_LとA_RとXしかないから
A_Lの事象は確率a_n
A_RとXの事象は確率1-a_n
やな。
そしたら図をかいて
n+1番目のA_Lが来るのはn番目が_L以外のA_RかXのときに次に1/2の確率でAAが出たときやから
a_(n+1)=1/2・(1-a_n)
ってわかるねん。
これ後は解いて
a_n=1/3+1/6・(-1/2)^(n-1)
やな。
後は求める確率はA_RとA_Lになる場合の和やから
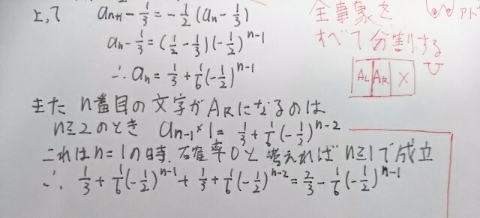
n番目の文字がA_Rになるのは
n≧2のときにn-1番目でA_Lが出たときにn番目がA_Rに自動的になるから。
a_(n-1)×1=1/3+1/6(-1/2)^(n-2)
やな。
しかもこれはn=1を代入すると0になるから1番目にはA_Rがこないってことを考えるとn≧1で使って大丈夫やな。
これで求める確率は
1/3+1/6・(-1/2)^(n-1)+1/3+1/6(-1/2)^(n-2)
=2/3-1/6・(-1/2)^(n-1)
やな。
(2)

n-1番目がA_Rでn番目がBのときやけどこれはさっきA_Rの場合を求めたからnをn-1にして
{1/3+1/6(-1/2)^(n-1)}×1/6
=1/18+1/9・(-1/2)^(n-1)
こうやって計算がわけわからんことなったら事象の分け方を変えてみると簡単になることもあるから選択肢に入れてくれたらええわ。
そしたらあれやな。
もう一つの方針を紹介しとこか。
こっちもよく使うねん。
確率の漸化式を立てる問題は
後ろに挿入することが多いねんけど
後ろに挿入するか、前に挿入するかもあって
東大は前に挿入することも多いねんl
例えばこの確率と漸化式の問題、東京大学2010年度文理共通第三問
とかな。
前に挿入するような問題は難しい問題やけどな。

求める確率をp_nとしよか
最初の1回が1文字であるXか
2文字であるAAで事象を分けるねん。
1回目が1文字のXのときはそこからn-1番目にAが出てこればええから
n-1回でn-1番目にAが出ると言うことでp_(n-1)やな。
1回目が2文字のAAのときからそこからn-2番目にAが出てこればよいから、n-2回でn-2番目にAが出てから残り1回は何でもええな。
それで
p_n=1/2・p_(n-1)+1/2・p_(n-2)・1
後は
p_1=1/2で
p_2=1/2+1/2・1/2=3/4
で解いたらええわ。
後は画像見ててください。
(2)
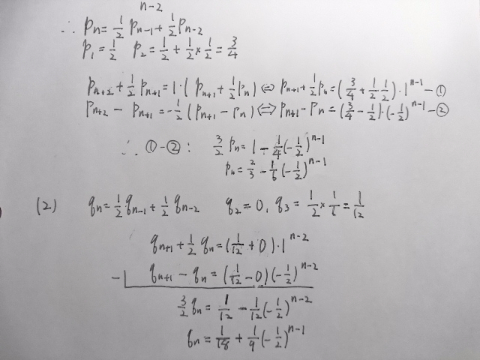
後は漸化式が同じやから、簡単やな。
東京大学の入試の数学の過去問の解説
- 関連記事
-
テーマ:大学受験 - ジャンル:学校・教育
|