かいき‐ぶんせき〔クワイキ‐〕【回帰分析】
回帰分析
回帰分析
・説明変数と目的変数の関係を回帰式で表し、目的変数が説明変数によってどの程度説明できるかを定量的に分析することである。
・回帰式は、y=ax+b(x:説明変数、y:目的変数)で表される。
・目的変数とは予測や要因分析を行う変数のことで、説明変数とは目的変数に影響を与えると考えられる変数のことである。
・回帰式を求めるのに変数a、切片bを推定する。推定には最小二乗法を用いる。最小二乗法は、観察された各点(x,y)と回帰線上の各点(x,yi)との残差dの平方和が最小となる直線を求める方法である。
・回帰分析は、予測・要因分析等に用いられる。例えば、過去の生産量と製造費用のデータから回帰式を求め、将来の生産量に対する製造費用の予測に活用される。この場合、生産量(x)に対する製造費用(y)の過去のデータから回帰式を推定する。生産量(x)1単位当りの製造費用(y)がどれ程増加するかを示す傾きaは変動費、切片bは固定費となる。将来の生産量(x1)を回帰式に代入すると将来の製造費用(y1)が導かれる。
・予測をする際には、回帰式の精度の良さの尺度となる決定係数(0~1の値)が1に近い(当てはまりが良い)のが望ましい。
・また回帰分析は、因果関係が想像される2つの変数の関係を調べるのに用いられるが、回帰式は、ある変数が増加(減少)すれば、もう一方の変数が増加(減少)するという関係性を示しているだけで、変数間に因果関係が本当に存在するかは注意して判断しなければならない。
回帰分析 regression analysis
回帰分析
【英】:regression analysis
概要
目的変数といわれる1つの変数と説明変数といわれる変数の間の関数関係を求める方法. 説明変数が1つである場合を単回帰分析, 複数である場合を重回帰分析といい, 説明変数の関数を回帰式という. その評価としては, 目的変数の値と関数の値の差の二乗和を用いることが多いが, 差の絶対値を用いることもある. 推測統計では, 回帰式を求めることは, 目的変数の期待値の推定に当たる.
詳説
分析の対象に対して, 複数の間隔尺度変数についての値(長さ, 時間などのいわゆる計量値)が得られているとする. 変数は, 一つの目的変数といくつかの説明変数に分かれていて, 目的変数とできるだけ近い値をとる説明変数の関数を求めるのを回帰分析という. 説明変数が一つである場合を単回帰分析, 二つ以上である場合を重回帰分析という.
[回帰式]
説明変数の関数を回帰式という. 説明変数を ,目的変数を
,目的変数を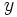 とする. 回帰式には, 通常, 次のような線形式が用いられる.
とする. 回帰式には, 通常, 次のような線形式が用いられる.

 を回帰係数といい, これを求めるのが目的である. なお, ここでの線形式は, 値を求める係数
を回帰係数といい, これを求めるのが目的である. なお, ここでの線形式は, 値を求める係数 に関して線形であることを示している. したがって, 説明変数の間には, たとえば,
に関して線形であることを示している. したがって, 説明変数の間には, たとえば,  のように, 線形以外の関係があってもよい. 非線形回帰式 [4] が用いられることもあるが, ここでは, 線形回帰式に限ることにする.
のように, 線形以外の関係があってもよい. 非線形回帰式 [4] が用いられることもあるが, ここでは, 線形回帰式に限ることにする.
[残差]
分析の対象の数を とし,
とし,  番目 (
番目 ( ) の対象の
) の対象の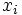 ,
, 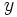 の値, いわゆるデータを
の値, いわゆるデータを ,
,  とする. 変数
とする. 変数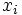 に
に 番目の対象の値
番目の対象の値 を代入したときの回帰式の値を
を代入したときの回帰式の値を , すなわち,
, すなわち,

とすると,

回帰式の評価は, 残差の関数を用いて行われる. 代表的な評価関数を以下に挙げる.

(2) 絶対偏差の和


いずれの評価関数も, 小さい方がよいので, 最小にする回帰式を最適とする.
SSDを最小にする回帰式(回帰係数)を求めるのを最小二乗法という. SSDは,  に関する 凸二次関数であるから, これらで偏微分した式を0とおいて得られる連立一次方程式を解けばよい. この連立一次方程式を正規方程式という.
に関する 凸二次関数であるから, これらで偏微分した式を0とおいて得られる連立一次方程式を解けばよい. この連立一次方程式を正規方程式という.
線形式の絶対値の和を最小にすることも, 線形式の絶対値の最大値を最小にする ことも, 線形計画問題に変形できることにより, SADを最小にする回帰式も, MAD を最小にする回帰式も, 線形計画問題を解くことによって得られる [2]. とくに, 一対比較の結果によるデータである場合は, ネットワーク計画問題に変形できる[3].
回帰分析は, 狭い意味では, 推測統計における解析法である. 説明変数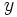 が確率変数
が確率変数 の実現値であって,
の実現値であって,  の期待値
の期待値![E[Y]\,](http://cdn.weblio.jp/e7/img/dict/orjtn/00d6360949c0c9ef3bf064bf8f31f447.png) が次のように説明変数の関数で表されるとする.
が次のように説明変数の関数で表されるとする.
![E[Y]=\beta_0+\beta_1 x_1+\beta_2 x_2+\cdots+\beta_m x_m
\,](http://cdn.weblio.jp/e7/img/dict/orjtn/5b5ad516cc268359869ca8d90291494b.png)
このとき, 回帰係数を求めることは, 未知定数 を推定することに当たる.
を推定することに当たる.  に対応する確率変数を
に対応する確率変数を とする, すなわち,
とする, すなわち,  が確率変数
が確率変数 の実現値と考えられるとき,
の実現値と考えられるとき,  の分布について, 分散が一定などの前提条件をおくと, 最小二乗法は, 望ましい推定法であることが証明されている [1].
の分布について, 分散が一定などの前提条件をおくと, 最小二乗法は, 望ましい推定法であることが証明されている [1].
[1] C. R. Rao, Linear Statistical Inference and Its Applications, John Wiley & Sons, 1973.
[2] T. S. Arthanari and Y. Dodge, Mathematical Programming in Statistics, John Wiley & Sons, 1981.
[3] 古林隆, 佐藤俊之, 鈴木政志, 「一対比較データのネットワーク計画法的解析」, 『日本オペレーションズ・リサーチ学会1991年度春季研究発表会アブストラクト集』, 112-113, 1991.
[4] N. R. Draper and H. Smith, Applied Regression Analysis, John Wiley & Sons, 1966.
回帰分析
「回帰分析」の例文・使い方・用例・文例
「回帰分析」に関係したコラム
-
線形回帰チャネルとは、線形回帰分析の1つで線形回帰線の上部と下部に線を引いたものです。一般的にFXやCFDなどで取引される銘柄の価格は、線形回帰チャネル内に収まりながら推移します。線形回帰チャネルは、...
- 回帰分析のページへのリンク


