Pojdi na vsebino

Seznam modelov Wenningerjevih poliedrov

Iz Wikipedije, proste enciklopedije

Seznam modelov Wenningerjevih poliedrov vsebuje uniformne in stelirane poliedre iz knjige Polyhedron Models (Modeli poliedrov), katere avtor je Magnus Wenninger (rojen 1919).

Platonska telesa (pravilna) W1 do W5

[uredi | uredi kodo]
zap. štev. ime slika ime duala slika duala Wythoffov simbol slika oglišč
in Schläflijev simbol 		simetrijska grupa U# K# V E F vrsta stranskih ploskev
1 tetraeder tetraeder 3|2 3
{3,3} 		Td U01 K06 4 6 4 4{3}
2 oktaeder heksaeder 4|2 3
{3,4} 		Oh U05 K10 6 12 8 8{3}
3 heksaeder (kocka) oktaeder 3|2 4
{4,3} 		Oh U06 K11 8 12 6 6{4}
4 ikozaeder dodekaeder 5|2 3
{3,5} 		Ih U22 K27 12 30 20 20{3}
5 dodekaeder ikozaeder 3|2 5
{5,3} 		Ih U23 K28 20 30 12 12{5}

Arhimedska telesa (polpravilna) W6 do W18

[uredi | uredi kodo]
zap. štev. ime slika ime duala slika duala Wythoffov simbol slika oglišča simetrijska grupa U# K# V E F vrsta stranskih ploskev
6 prisekani tetraeder triakisni tetraeder Triakis tetrahedron 2 3|3
3.6.6 		Td U02 K07 12 18 8 4{3} + 4{6}
7 prisekani oktaeder tetrakisni heksaeder Tetrakis hexahedron 2 4|3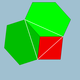
4.6.6 		Oh U08 K13 24 36 14 6{4} + 8{6}
8 prisekani heksaeder triakisni oktaeder Triakis octahedron 2 3|4
3.8.8 		Oh U09 K14 24 36 14 8{3} + 6{8}
9 prisekani ikozaeder 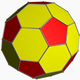pentakisni dodekaeder Pentakis dodecahedron 2 5|3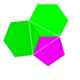
5.6.6 		Ih U25 K30 60 90 32 12{5} + 20{6}
10 prisekani dodekaeder triakisni ikozaeder Triakis icosahedron 2 3|5
3.10.10 		Ih U26 K31 60 90 32 20{3} + 12{10}
11 kubootaeder rombski dodekaeder Rhombic dodecahedron 2|3 4
3.4.3.4 		Oh U07 K12 12 24 14 8{3} + 6{4}
12 ikozododekaeder rombski triakontaeder Rhombic triacontahedron 2|3 5
3.5.3.5 		Ih U24 K29 30 60 32 20{3} + 12{5}
13 mali rombokubooktaeder deltoidni ikozitetraeder Deltoidal icositetrahedron 3 4|2
3.4.4.4 		Oh U10 K15 24 48 26 8{3}+(6+12){4}
14 mali rombiikozidodekaeder deltoidni heksekontaeder Deltoidal hexecontahedron 3 5|2
3.4.5.4 		Ih U27 K32 60 120 62 20{3} + 30{4} + 12{5}
15 veliki rombikubooktaeder
(rombiprisekani kubooktaeder)
(prisekanikubooktaeder) 		disdiakisni dodekaeder Disdyakis dodecahedron 2 3 4|
4.6.8 		Oh U11 K16 48 72 26 12{4} + 8{6} + 6{8}
16 veliki rombiikozidodekaeder
(rombiprisekaniikozidodekaeder)
(prisekani ikozidodekaeder) 		disdiakisni triakontaeder Disdyakis triacontahedron 2 3 5|
4.6.10 		Ih U28 K33 120 180 62 30{4} + 20{6} + 12{10}
17 prirezana kocka pentagonalni ikozitetraeder Pentagonal icositetrahedron |2 3 4
3.3.3.3.4 		O U12 K17 24 60 38 (8 + 24){3} + 6{4}
18 prirezani dodekaeder pentagonalni heksekontaeder Pentagonal hexecontahedron |2 3 5
3.3.3.3.5 		I U29 K34 60 150 92 (20 + 60){3} + 12{5}

Kepler-Poinsotovi poliedri (pravilni zvezdni poliedri) W20, W21, W22 in W41

[uredi | uredi kodo]
zap. štev. ime slika dualno ime dualna slika Wythoffov simbol slika oglišča
in Schläflijev simbol 		simetrijska grupa U# K# V E F vrsta facete
20 mali stelirani dodekaeder veliki dodekaeder 5|25/2
{5/2,5} 		Ih U34 K39 12 30 12 12{5/2}
21 veliki dodekaeder mali stelirani dodekaeder 5/2|2 5
{5,5/2} 		Ih U35 K40 12 30 12 12{5}
22 veliki stelirani dodekaeder veliki ikozaeder 3|25/2
{5/2,3} 		Ih U52 K57 20 30 12 12{5/2}
41 veliki ikozaeder
(16. Stelacija ikozaedra) 		veliki stelirani dodekaeder 5/2|2 3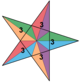
{3,5/2} 		Ih U53 K58 12 30 20 20{3}

Pojasnila:

  • U# pomeni številko uniformnega številčenja (U01 - U80)
  • K# pomeni številko Kaleido številčenja (K01 – K80)

V je število oglišč

E je število robov

F je število stranskih ploskev

Stelacije: modeli W19 do W66

[uredi | uredi kodo]

Stelacije oktaedra

[uredi | uredi kodo]
zap. štev. ime grupa simetrije slika facete
2 oktaeder
(pravilni) 		Oh
19 stelirani oktaeder
(zgrajen iz dveh tetraedrov) 		Oh

Stelacije dodekaedra

[uredi | uredi kodo]
zap. štev. ime simetrijska grupa slika facete
5 dodekaeder (pravilni) Ih
20 mali stelirani dodekaeder (regular)
(prva stelacija dodekaedra) 		Ih
21 veliki dodekaeder (regular)
(druga stelacija dodekaedra) 		Ih
22 veliki zvezdni dodekaeder (pravilni)
(tretja stelacija dodekaedra) 		Ih

Stelacije ikozaedra

[uredi | uredi kodo]
zap. štev. ime grupa simetrije slika facete
4 ikozaeder (pravilni) Ih
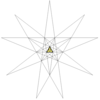
23 sestav petih oktaedrov
(prva sestavljena stelacija ikozaedra) 		Ih
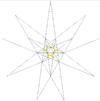
24 sestav petih tetraedrov
(druga sestavljena stelacija ikozaedra) 		I
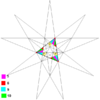
25 sestav desetih tetraedrov
(tretja sestavljena stelacija ikozaedra) 		Ih
26 mali triambski ikozaeder
(prva stelacija ikozaedra)
(triakisni ikozaeder) 		Ih
27 druga stelacija ikozaedra Ih
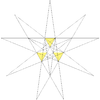
28 izkopani dodekaeder
(tretja stelacija ikozaedra) 		Ih
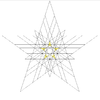
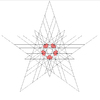
29 četrta stelacija ikozaedra Ih
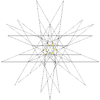
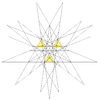
30 peta stelacija ikozaedra Ih
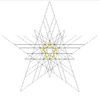
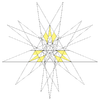
31 šesta stelacija ikozaedra Ih
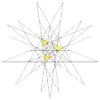
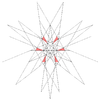
32 sedma stelacija ikozaedra Ih
33 osma stelacija ikozaedra Ih
34 deveta stelacija ikozaedra
veliki triambski ikozaeder
 Ih
35 deseta stelacija ikozaedra I
36 enajsta stelacija ikozaedra I
37 dvanajsta stelacija ikozaedra Ih
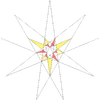
38 trinajsta stelacija ikozaedra I
39 štirinajska stelacija ikozaedra I
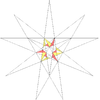
40 petnajsta stelacija ikozaedra I
41 veliki ikozaeder (pravilni)
(šestnajsta stelacija ikozaedra) 		Ih
42 končna stelacija ikozaedra Ih

Stelacije kubooktaedra

[uredi | uredi kodo]
zap.štev ime grupa simetrije slika facete (oktaederske ravnine) facete (ravnine kocke)
11 kubooktaeder (pravilni) Oh
43 sestav kocke in oktaedra
(prva stelacija kubooktaedra) 		Oh
44 druga stelacija kubooktaedra Oh
45 tretja stelacija kubooktaedra Oh
46 četrta stelacija kubooktaedra Oh

Stelacije ikozidodekaedra

[uredi | uredi kodo]
zap. štev. ime simetrijska grupa slika facete (ikozaederske ravnine) facete (dodekaederske ravnine)
12 ikozidodekaeder
(pravilni) 		Ih
47 (prva stelacija ikozidodekaedra)
sestav dodekaedra in ikozaedra 		Ih
48 druga stelacija ikozidodekaedra Ih
49 tretja stelacija ikozidodekaedra Ih
50 četrta stelacija ikozidodekaedra
(sestav malega steliranega dodekaedra
in triakisnega ikozaedra) 		Ih
51 peta stelacija ikozidodekaedra
(sestav malega steliranega dodekaedra
in petih oktaedrov) 		Ih
52 šesta stelacija ikozidodekaedra Ih
53 sedma stelacija ikozidodekaedra Ih
54 osma stelacija ikozidodekaedra
(sestav petih tetraedrov
in velikega dodekaedra) 		I
55 deveta stelacija ikozidodekaedra Ih
56 deseta stelacija ikozidodekaedra Ih
57 enajsta stelacija ikozidodekaedra Ih
58 dvanajsta stelacija ikozidodekaedra Ih
59 trinajsta stelacija ikozidodekaedra Ih
60 štirinajsta stelacija ikozidodekaedra Ih
61 sestav velikega steliranega dodekaedra in velikega ikozaedra Ih
62 petnajsta stelacija ikozidodekaedra Ih
63 šestnajsta stelacija ikozidodekaedra Ih
64 sedemnajsta stelacija ikozidodekaedra Ih
65 osemnajsta stelacija ikozidodekaedra Ih
66 devetnajsta stelacija ikozidodekaedra Ih

Uniformna nekonveksna telesa W67 do W119

[uredi | uredi kodo]
zap. štev. ime slika dualno ime dualna slika Wythoffov simbol slika oglišč simetrijska grupa U# K# V E F vrste stranskih ploskev
67 tetrahemiheksaeder tetrahemiheksakron 3/23|2
4.3/2.4.3		 Td U04 K09 6 12 7 4{3}+3{4}
68 oktahemioktaeder oktahemioktakron 3/23|3
6.3/2.6.3		 Oh U03 K08 12 24 12 8{3}+4{6}
69 mali kubikubooktaeder mali heksakronski ikozitetraeder 3/24|4
8.3/2.8.4		 Oh U13 K18 24 48 20 8{3}+6{4}+6{8}
70 mali ditrigonalni ikozidodekaeder mali triambski ikozaeder 3|5/23
(5/2.3)3		 Ih U30 K35 20 60 32 20{3}+12{5/2}
71 mali ikozikozidodekaeder mali ikozakronskihexekontaeder 5/23|3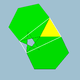
6.5/2.6.3		 Ih U31 K36 60 120 52 20{3}+12{5/2}+20{6}
72 mali dodeciikozidodekaeder mali dodekakronski hexekontaeder 3/25|5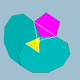
10.3/2.10.5		 Ih U33 K38 60 120 44 20{3}+12{5}+12{10}
73 dodekadodekaeder srednji rombski triakontaeder 2|5/25
(5/2.5)2		 Ih U36 K41 30 60 24 12{5}+12{5/2}
74 mali rombidodekaeder mali rombidodekakron 25/25|
10.4.10/9.4/3		 Ih U39 K44 60 120 42 30{4}+12{10}
75 prisekani veliki dodekaeder mali stelapentakisni dodekaeder 25/2|5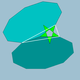
10.10.5/2		 Ih U37 K42 60 90 24 12{5/2}+12{10}
76 rombidodekadodekaeder srednji deltoidni heksekontaeder 5/25|2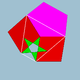
4.5/2.4.5		 Ih U38 K43 60 120 54 30{4}+12{5}+12{5/2}
77 veliki kubikubooktaeder veliki heksakroničniikozitetraeder 3 4|4/3
8/3.3.8/3.4		 Oh U14 K19 24 48 20 8{3}+6{4}+6{8/3}
78 kubohemioktaeder heksahemioktakron 4/34|3
6.4/3.6.4		 Oh U15 K20 12 24 10 6{4}+4{6}
79 kubiprisekanikoboooktaeder
(kuboprisekani kubooktaeder)		 tetradiakisni heksaeder 4/33 4|
8/3.6.8		 Oh U16 K21 48 72 20 8{6}+6{8}+6{8/3}
80 Ditrigonal dodecadodecahedron srednji triambski ikozaeder 3|5/35
(5/3.5)3		 Ih U41 K46 20 60 24 12{5}+12{5/2
81 veliki ditrigonalnidodeciikozidodekaeder veliki ditrigonalni dodekakronskiheksekontaeder 3 5|5/3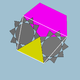
10/3.3.10/3.5		 Ih U42 K47 60 120 44 20{3}+12{5}+12{10/3}
82 mali ditrigonalni dodeciikozidodekaeder 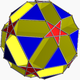mali ditrigonalni dodekakronični helsekontaeder 5/33|5
10.5/3.10.3		 Ih U43 K48 60 120 44 20{3}+12{5/2}+12{10}
83 ikozidodekaeder srednji izakronski heksekontaeder 5/35|3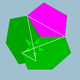
6.5/3.6.5		 Ih U44 K49 60 120 44 12{5}+12{5/2}+20{6}
84 ikoziprisekanidodekadodekaeder
(ikozidokekaprisekani ikozidodekaeder)		 tridiakisni ikozaeder 5/33 5|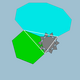
10/3.6.10		 Ih U45 K50 120 180 44 20{6}+12{10}+12{10/3}
85 nekoveksni veliki rombikubooktaeder
(kvazirombokubooktaeder)		 veliki deltoidni ikozitetraeder 3/24|2
4.3/2.4.4		 Oh U17 K22 24 48 26 8{3}+(6+12){4}
86 mali rombiheksaeder mali rombiheksakron 3/22 4|
4.8.4/3.8		 Oh U18 K23 24 48 18 12{4}+6{8}
87 veliki ditrigonalni ikozidodekaeder veliki triambskiikozaeder 3/2|3 5
(5.3.5.3.5.3)/2		 Ih U47 K52 20 60 32 20{3}+12{5}
88 veliki ikoziikozidodekaeder 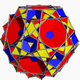veliki ikozakronskiheksekontaeder 3/25|3
6.3/2.6.5		 Ih U48 K53 60 120 52 20{3}+12{5}+20{6}
89 mali ikozihemidodekaeder mali ikozihemidodekakron 3/23|5
10.3/2.10.3		 Ih U49 K54 30 60 26 20{3}+6{10}
90 mali dodeciikozaeder mali dodeciikozakron 3/23 5|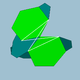
10.6.10/9.6/5		 Ih U50 K55 60 120 32 20{6}+12{10}
91 mali dodekahemidodekaeder 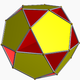mali dodekahemidodekakron 5/45|5
10.5/4.10.5		 Ih U51 K56 30 60 18 12{5}+6{10}
92 stelirani prisekani heksaeder
(kvaziprisekani heksaeder)		 veliki trikisni oktaeder 2 3|4/3
8/3.8/3.3		 Oh U19 K24 24 36 14 8{3}+6{8/3}
93 veliki prisekani kubooktaeder
(kvaziprisekani kubooktaeder)		 veliki disdiakisnidodekaeder 4/32 3|
8/3.4.6		 Oh U20 K25 48 72 26 12{4}+8{6}+6{8/3}
94 veliki ikozidodekaeder veliki rombski triakontaeder 2|5/23
(5/2.3)2		 Ih U54 K59 30 60 32 20{3}+12{5/2}
95 prisekani veliki ikozaeder veliki stelapentakisni dodekaeder 25/2|3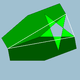
6.6.5/2		 Ih U55 K60 60 90 32 12{5/2}+20{6}
96 rombiikozaeder Rhombicosacron 25/23|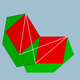
6.4.6/5.4/3		 Ih U56 K61 60 120 50 30{4}+20{6}
97 mali stelirani prisekani dodekaeder
(kvaziprisekani mali stelirani dodekaeder)		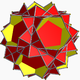 veliki pentakisni dodekaeder 2 5|5/3
10/3.10/3.5		 Ih U58 K63 60 90 24 12{5}+12{10/3}
98 prisekani dodekadodekaeder
(kvaziprisekani dodekaeder)		 srednji disdiakisni triakontaeder 5/32 5|
10/3.4.10		 Ih U59 K64 120 180 54 30{4}+12{10}+12{10/3}
99 veliki dodeciikozidodekaeder 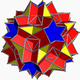veliki dodekakronskiheksekontaeder 5/23|5/3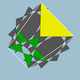
10/3.5/2.10/3.3		 Ih U61 K66 60 120 44 20{3}+12{5/2}+12{10/3 }
100 Small dodecahemicosahedron mali dodekahemiikozakron 5/35/2|3
6.5/3.6.5/2		 Ih U62 K67 30 60 22 12{5/2}+10{6}
101 veliki dodeciikozieder veliki dodecikosakron 5/35/23|
6.10/3.6/5.10/7		 Ih U63 K68 60 120 32 20{6}+12{10/3}
102 veliki dodekahemiikozaeder veliki dodekahemikosakron 5/45|3
6.5/4.6.5		 Ih U65 K70 30 60 22 12{5}+10{6}
103 veliki rombiheksaeder veliki rombiheksakron 4/33/22|
4.8/3.4/3.8/5		 Oh U21 K26 24 48 18 12{4}+6{8/3}
104 veliki stelirani prisekani dodekaeder
(kvazoprisekani veliki stelirani dodekaeder)		 veliki triakisni ikozaeder 2 3|5/3
10/3.10/3.3		 Ih U66 K71 60 90 32 20{3}+12{10/3}
105 nekonveksni veliki rombiikozidodekaeder
(kvazirombiikozidodekaeder)		 veliki deltoidni heksekontaeder 5/33|2
4.5/3.4.3		 Ih U67 K72 60 120 62 20{3}+30{4}+12{5/2}
106 veliki ikozihemidodekaeder veliki ikozihemidodekakron 3 3|5/3
10/3.3/2.10/3.3		 Ih U71 K76 30 60 26 20{3}+6{10/3}
107 veliki dodekahemidodekaeder] veliki dodekahemidodekakron 5/35/2|5/3
10/3.5/3.10/3.5/2		 Ih U70 K75 30 60 18 12{5/2}+6{10/3}
108 veliki prisekaniikozidodekaeder
(veliki kvaziprisekani ikozidodekaeder)		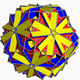 veliki disdiakisnitriakontaeder 5/32 3|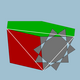
10/3.4.6		 Ih U68 K73 120 180 62 30{4}+20{6}+12{10/3}
109 veliki rombidodekaeder veliki dodekakron 3/25/32|
4.10/3.4/3.10/7		 Ih U73 K78 60 120 42 30{4}+12{10/3}
110 mali prirezaniikoziikozidodekaeder mali heksagonalni heksekontaeder |5/23 3
3.3.3.3.3.5/2		 Ih U32 K37 60 180 112 (40+60){3}+12{5/2}
111 prirezani dodekadodekaeder srednji pentagonalni heksekontaeder |25/25
3.3.5/2.3.5		 I U40 K45 60 150 84 60{3}+12{5}+12{5/2}
112 prirezani ikozidodekadodekaeder 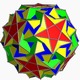Medial hexagonal hexecontahedron |5/33 5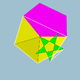
3.3.3.3.5.5/3		 I U46 K51 60 180 104 (20+6){3}+12{5}+12{5/2}
113 veliki obrnjeni prirezani ikozododekaeder veliki obrnjeni pentagonalni heksekontaeder |5/32 3
3.3.3.3.5/3		 I U69 K74 60 150 92 (20+60){3}+12{5/2}
114 obrnjeni prirezani dodekadokekaeder 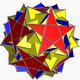srednji obrnjeni pentagonalni heksekontaeder |5/32 5
3.5/3.3.3.5		 I U60 K65 60 150 84 60{3}+12{5}+12{5/2}
115 veliki prirezani dodeciikozidodekaeder veliki heksagonalniheksekontaeder |5/35/23
3.5/3.3.5/2.3.3		 I U64 K69 60 180 104 (20+60){3}+(12+12){5/2}
116 veliki prirezani ikozidodekaeder veliki pentagonalni heksekontaeder |25/25/2
3.3.3.3.5/2		 I U57 K62 60 150 92 (20+60){3}+12{5/2}
117 veliki retroprirezani ikozidodekaeder veliki pentagramski heksekontaeder |3/25/32
(3.3.3.3.5/3)/2		 I U74 K79 60 150 92 (20+60){3}+12{5/2}
118 mali retroprirezani ikoziikozidodekaeder mali heksegramski heksekontaeder |3/23/25/2
(3.3.3.3.3.5/2)/2		 Ih U72 K77 180 60 112 (40+60){3}+12{5/2}
119 veliki dirombiikozidodekaeder veliki dirombiikozidodekakron |3/25/335/2
(4.5/3.4.3.4.5/2.4.3/2)/2		 Ih U75 K80 60 240 124 40{3}+60{4}+24{5/2}
za različne oblike poliedrov z oznakami W001 - W119
    • 1 -18 za 5 konveksnih pravilnih in 13 konveksnih poliedrov polpravilnih
    • 20 – 22, 41 za 4 nekonveksne pravilne poliedre
    • 19 – 66 za specialnih 48 stelacij (nepravilni niso v tem seznamu)
    • 67 – 119 za 53 nekonveksnih uniformnih poliedrov
  • U# pomeni številko uniformnega številčenja (U01 - U80)
  • K# pomeni številko Kaleido številčenja (K01 – K80)

V je število oglišč E je število robov F je število stranskih ploskev

Zunanje povezave

[uredi | uredi kodo]


Pridobljeno iz »https://sl.wikipedia.org/w/index.php?title=Seznam_modelov_Wenningerjevih_poliedrov&oldid=6323434«