展開形ゲーム
【英】:game in extensive form
概要
プレイヤーの手番の系列をグラフ理論の有向木を用いて表現するゲームのモデル. 木の分岐点はプレイヤーの手番, 枝はプレイヤーの選択肢または行動を表す. ゲームのプレイは木の初期点から始まり木の1つの終点に到達して終了する. プレイヤーの同時的な意思決定を定式化する戦略形ゲームに対して, 展開形ゲームはプレイヤーの動学的な意思決定問題を分析するために用いられる.代表的な均衡概念に部分ゲーム完全均衡, 完全均衡や逐次均衡がある.
詳説
展開形ゲーム (game in extensive form) はプレイヤーの手番の系列をゲームの木 (game tree) を用いて表現するモデルである. ゲームの木 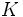 はグラフ理論でいう有向木で, 木の分岐点はプレイヤーが選択肢を選ぶ手番, 枝はプレイヤーの選択肢あるいは行動を表す. 木の始点から終点までの経路をゲームの1つのプレイという.
はグラフ理論でいう有向木で, 木の分岐点はプレイヤーが選択肢を選ぶ手番, 枝はプレイヤーの選択肢あるいは行動を表す. 木の始点から終点までの経路をゲームの1つのプレイという.
プレイヤー分割 ![P=[P_{0}, P_{1}. \cdots, P_{n}]\,](http://cdn.weblio.jp/e7/img/dict/orjtn/46480a553c91ba63b9dced354e9981a9.png) は, ゲームの木
は, ゲームの木 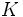 の分岐点の全体を
の分岐点の全体を 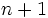 個の部分集合に分割する.
個の部分集合に分割する.  はプレイヤー
はプレイヤー  の手番の集合を表す.
の手番の集合を表す.  に含まれる手番は偶然手番とよばれ, プレイヤーの意思とは無関係な偶然機構によって枝が選択される. 天候やトランプゲームでランダムにカードを配るなどは, 偶然手番の典型的な例である. 偶然手番に対しては枝の選択を行なう確率分布
に含まれる手番は偶然手番とよばれ, プレイヤーの意思とは無関係な偶然機構によって枝が選択される. 天候やトランプゲームでランダムにカードを配るなどは, 偶然手番の典型的な例である. 偶然手番に対しては枝の選択を行なう確率分布  が付与される.
が付与される.
ゲームの情報分割 ![U=[U_{0}, U_{1}, \cdots, U_{n}]\,](http://cdn.weblio.jp/e7/img/dict/orjtn/55af3504bbccf5d27b87169c96ffbf2f.png) は,プレイヤー分割
は,プレイヤー分割 の細分割である.各
の細分割である.各  に対して
に対して ![U_{i}=[u_{i1}, u_{i2}, \cdots, u_{im_{i}}]\,](http://cdn.weblio.jp/e7/img/dict/orjtn/34b17d51ea9de9c362aeab2e43db317f.png) はプレイヤー
はプレイヤー  の手番の集合
の手番の集合  を
を  個の非空な部分集合に分割する.
個の非空な部分集合に分割する.  に属する部分集合
に属する部分集合  をプレイヤー
をプレイヤー  の情報集合 (information set) という.プレイヤーは行動を選択するとき,自分の手番がどの情報集合に属するかは知っているが,情報集合の中のどの分岐点であるかは知らない.
の情報集合 (information set) という.プレイヤーは行動を選択するとき,自分の手番がどの情報集合に属するかは知っているが,情報集合の中のどの分岐点であるかは知らない.
ゲームの利得関数 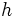 は,ゲームの木
は,ゲームの木 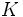 の各終点
の各終点 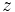 に対してプレイヤーの利得ベクトル
に対してプレイヤーの利得ベクトル  を対応させる.
を対応させる.
形式的には, 展開形ゲーム 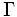 は以上の5つの要素の組
は以上の5つの要素の組  によって定義される. これらの5つの構成要素をゲームのルールという.
によって定義される. これらの5つの構成要素をゲームのルールという.
 |
| 図1:展開形ゲーム |
展開形ゲームの例として図1を考える.プレイヤー1と2の情報分割はそれぞれ ![U_{1}=[u_{1}], U_{2}=[u_{21}, u_{22}]\,](http://cdn.weblio.jp/e7/img/dict/orjtn/d75ec15e43d873d881944416d1a943cb.png) である.図1では最初にプレイヤー1がRとLの2つの行動のうち1つを選択する. 次に, プレイヤー2はプレイヤー1の選択を知った上で, RとLのうちから1つの行動を選択する.ゲームは4つの終点をもち, 終点に付与されている利得ベクトルは上の数字がプレイヤー1の利得, 下の数字がプレイヤー2の利得を表す.
である.図1では最初にプレイヤー1がRとLの2つの行動のうち1つを選択する. 次に, プレイヤー2はプレイヤー1の選択を知った上で, RとLのうちから1つの行動を選択する.ゲームは4つの終点をもち, 終点に付与されている利得ベクトルは上の数字がプレイヤー1の利得, 下の数字がプレイヤー2の利得を表す.
図1のゲームのように, プレイヤーのすべての情報集合がただ1つの分岐点から成るゲームを完全情報ゲーム (game with perfect information) といい, そうでないゲームを不完全情報ゲーム (game with imperfect information) という. 完全情報ゲームでは, すべての手番においてプレイヤーはゲームの過去のプレイの経過を完全に知った上で行動を選択できる. チェスや将棋は完全情報ゲームである.
展開形ゲームの部分木でそれ自身が展開形ゲームの構造をもつものを部分ゲームという. 図1のゲームは, 情報集合  と
と  から始まる2つの部分ゲームをもつ.
から始まる2つの部分ゲームをもつ.
プレイヤー  の各情報集合
の各情報集合  に対して
に対して 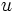 における選択肢の集合上の1つの確率分布
における選択肢の集合上の1つの確率分布  を対応させる関数
を対応させる関数  をプレイヤー
をプレイヤー  の行動戦略 (behavior strategy) という. 特に, すべての情報集合に対して1つの選択肢を確定的に対応させる行動戦略を純戦略という.
の行動戦略 (behavior strategy) という. 特に, すべての情報集合に対して1つの選択肢を確定的に対応させる行動戦略を純戦略という.
例えば, 図1のゲームにおいて, プレイヤー1の純戦略  はRとLの2通りであり, プレイヤー2の純戦略
はRとLの2通りであり, プレイヤー2の純戦略  は, RR, RL, LR, LLの4通りである. ただし, 前の文字は情報集合
は, RR, RL, LR, LLの4通りである. ただし, 前の文字は情報集合  でとる行動, 後の文字は情報集合
でとる行動, 後の文字は情報集合  でとる行動を表す. 図1の展開形ゲームから, プレイヤーの純戦略と利得の関係によって図2のような戦略形ゲームを作ることができる.
でとる行動を表す. 図1の展開形ゲームから, プレイヤーの純戦略と利得の関係によって図2のような戦略形ゲームを作ることができる.
| |||||
| R |
| ||||
| L |
|
図2:図1の展開形ゲームから作られた戦略形ゲーム
プレイヤーの行動分析のための最も基本的なゲームの解の概念は, ナッシュ (J. F. Nash) によって定義された非協力均衡点である. 一般にナッシュ均衡と呼ばれている. 展開形ゲームの行動戦略の組  がナッシュ均衡であるとは,すべてのプレイヤー
がナッシュ均衡であるとは,すべてのプレイヤー  のすべての行動戦略
のすべての行動戦略  に対して,
に対して,

が成り立つことである. ただし,  は
は  からプレイヤー
からプレイヤー  だけが戦略を
だけが戦略を  から
から  に変更してできる行動戦略の組を表し,
に変更してできる行動戦略の組を表し,  はプレイヤー i の期待利得関数を表す.
はプレイヤー i の期待利得関数を表す.
完全情報ゲームのナッシュ均衡は, 最初に, 終点に一番近い分岐点で, その手番のプレイヤーの利得を最大にする最適戦略を求め, 以下順次, ゲームの木を後向きに解くことによって計算できる. 例えば, 図1のゲームで情報集合  と
と  におけるプレイヤー2の最適戦略はそれぞれLとRである. このとき, 情報集合
におけるプレイヤー2の最適戦略はそれぞれLとRである. このとき, 情報集合  におけるプレイヤー1の最適戦略はRであり, 純戦略の組 (R, LR) はゲームのナッシュ均衡である. このようなナッシュ均衡の計算方法を, ゲームの後向き帰納法という. キューン (H. Kuhn) は,
におけるプレイヤー1の最適戦略はRであり, 純戦略の組 (R, LR) はゲームのナッシュ均衡である. このようなナッシュ均衡の計算方法を, ゲームの後向き帰納法という. キューン (H. Kuhn) は,  人完全情報ゲーム は純戦略の範囲で少なくとも1つのナッシュ均衡をもつことを証明した [1].
人完全情報ゲーム は純戦略の範囲で少なくとも1つのナッシュ均衡をもつことを証明した [1].
図1のゲームは (R, LR) の他に図2の利得行列で*をつけたナッシュ均衡をもつ. しかし, これらのナッシュ均衡は均衡プレイ上にない分岐点ではプレイヤーの最適戦略を導かないという欠点をもつ. ゼルテン (R. Selten) はナッシュ均衡のこのような欠点を解消するために, より強い均衡概念として, すべての部分ゲーム上にナッシュ均衡を導く部分ゲーム完全均衡 (subgame perfect equilibrium) を定義した [3].
ゼルテンの研究以後, 展開形ゲームの理論は大きく進展し, 現在, ゲーム的状況におけるプレイヤーの戦略的行動を解明する基礎理論としてORや経済学を始め広範囲の分野に応用されている.
[1] H. W. Kuhn, "Extensive Games and the Problem of Information," in H. W. Kuhn and A. Tucker(eds.), Contributions to the Theory of Games, Vol. II, Annals of Mathematics Studies 28, Princeton University Press, 1953, 193-216.
[3] R. Selten, "Reexamination of the Perfectness Concept for Equilibrium Points in Extensive Games," International Journal of Game Theory, 4 (1975), 25-55.
展開型ゲーム
展開型ゲーム(てんかいがたゲーム、英: Extensive-form game)とは、ゲームの表現形式のひとつであり、ゲームの木と呼ばれるグラフの形式で表現されたものである。ゲームの表現形式には展開型と標準型(または戦略型)と特性関数型(または提携型)の3種がある。ある非協力ゲームは展開型でも標準型でも表現できるが、展開型の方が情報量が多い。特性関数型は特に協力ゲームの表現に使われる[1][2][3][4]。
展開型ゲームは、ゲームの木、プレイヤー分割、偶然手番の確率分布族、情報分割、利得関数の5つの要素で記述できる。
ゲームの木
ゲームの木は点で示されるノードと2点を結ぶ有向線分である枝とから成る。ノードは状態とも呼ばれ、ゲームのひとつの局面を表す。枝は一人のプレイヤーの意志または偶然による選択により、あるノードから別のノードへ遷移できることを示すもので選択肢(alternative)とも呼ばれる。ノードは分岐点と頂点に分けられる。頂点はそこから枝が出ていないノード、すなわちゲームが終了した局面を示す点であり、各プレイヤーの利得(pay off)が与えられている。利得は利得関数とも呼ばれ、プレイヤーの数だけの成分数を持つベクトル量として表せる。分岐点は頂点以外のノードであり、手番(move)とも呼ばれる。各手番では一人のプレイヤーの意志または偶然により、その手番から出ている選択肢のひとつが選択されてその先の手番に遷移する。偶然により選択がなされる手番を偶然手番と呼ぶ。またプレイヤー甲の意志で選択がなされる手番を甲の手番と呼ぶ。プレイヤー分割とは手番の集合を各プレイヤーの手番に分割したものである。偶然手番の確率分布族とは偶然手番での確率分布を定めたものである。そこに遷移する選択肢がひとつもない分岐点を底点と呼び、これはゲームの初期状態、つまり出発局面である。
以下に「奇数偶数ゲーム」(MorraまたはOdd-or-evenと呼ばれる)を例としてゲームの木を示す。これは、双方が偶数か奇数のどちらかを示し、示された数の和が偶数ならAの勝ちで奇数ならBの勝ちとするゲームである(外部リンクの英語版wikipedia参照)。
例示
各局面が、枝を選択するプレイヤー(偶然も含む)の他にどのようなもので定まるかの具体例をいくつか挙げる。チェスやダイヤモンドゲーム、連珠、リバーシなどでは各局面は盤面の各位置の駒の種類(空白も含む)で完全に定まる。将棋ではさらに各プレイヤーの持ち駒も含めれば完全に定まる。チェスや将棋では頂点は詰みやステイルメイトの局面であり、そこでの各プレイヤーの利得は例えば勝者が+1で敗者が-1と表せる。リバーシでは頂点は盤面全てに石が置かれた局面であり、利得は盤面にある各プレイヤーの駒(石)の個数である。碁では利得は、いわゆる地の数である。カードゲームでは各プレイヤーの手札と獲得した札、および場に晒されている場札および山札で局面が定まる。例えばコントラクトブリッジやホイストでは頂点は各プレイヤーの手札が無くなった局面であり、そこでの利得はそれまでに取ったトリック数である。カードゲームの利得には他にも、各プレイヤーが獲得していた札の枚数や点数、獲得した札の組み合わせで定まる点数などルールにより多様なものがある。
情報分割
情報分割(information partition)とは手番の集合を情報集合(information set)に分割したものである。プレイヤー甲の情報集合とは甲の手番から成る集合であり、ひとつの情報集合の中のある手番に居るとき、甲はその情報集合の中のどの手番に居るのかを知ることができない。
例えば多くのカードゲームでは各プレイヤーは自分の手札と場札しか知ることができず、他のプレイヤーの手札と山札は知ることができない。つまり自分がプレイしようとする時に、現在の局面はある複数の局面の中のどれかひとつであることしかわからない。このとき、自分の手札と場札はわかるが他の札の状態はわからないので、現在の局面には知らない札の組み合わせの数だけの可能性がある。これらの可能な局面つまり手番の全ての集合が情報集合になる。チェスなど多くのボードゲームのように自分の手番の状態を全て知ることができるゲームは、全ての情報集合がただひとつの手番を持つゲームと定義でき、このようなゲームを完全情報ゲーム(Game with perfect information)と呼ぶ。完全情報ゲームではないゲームを不完全情報ゲーム(Game with imperfect information)という。麻雀、七並べ、大富豪、UNOなどは相手の手札が見えないので不完全情報ゲームである。
同時手番ゲーム
ジャンケンのように各プレイヤーが同時に指すゲームを同時手番ゲームと呼ぶが、これは各プレイヤーが順番に指すが全員が指し終えるまでは他のプレイヤーの指し手が隠されている不完全情報ゲームと同値である。先に例示した「奇数偶数ゲーム」も同時手番ゲームの例である。
完全記憶ゲーム
全プレイヤーが自分の過去の選択肢を全て記憶しているゲームを完全記憶ゲーム(Game with perfect recall)と呼ぶ。完全情報ゲームは完全記憶ゲームである。完全記憶であり不完全情報であるゲームの木の例を図3に示す。また不完全記憶ゲームの木の例を図4に示す。図4のプレイヤーAのように一手前の記憶を喪失するプレイヤーは想像しにくいが、例えばプレイヤーAを2名のチームと考え、手番と手番では別のチーム員が指しチーム員同士は情報交換ができないとすれば、現実的な一例となる。
完備情報ゲーム
完備情報ゲーム(Game with complete information)という言葉もあり、これは全プレイヤーがゲームのルールすなわちゲームの木の全体像を知っているゲームである。現実の戦争や経済行為のゲームはほとんどが完備情報ゲームではない、すなわち不完備情報ゲーム(Game with imcomplete information)である。しかし不完備情報ゲームは、情報が不明な部分を偶然手番に置き換えることにより、完備情報ゲームとして表現し解析することができる。
展開型ゲームと標準型ゲーム
標準型ゲームは戦略型ゲームと呼ばれることもあり、各プレイヤーの選択肢の組合わせに対応した利得で表される。例えば「奇数偶数ゲーム」では各プレイヤーの選択肢は偶数か奇数かの2つであり4通りの組み合わせの利得を標準型で表すと図1Bのようになる。ここで一方のプレイヤーが先に選択肢を選び、他方のプレイヤーは何が選択されたかを知らずに自分の選択肢を選ぶと考えると展開型の表現になる。後手の手番での情報集合は2つの分岐点を含んでおり、このゲームは不完全情報ゲームだとわかる。標準型ゲームでの各プレイヤーの選択肢を純戦略と呼ぶ。単に戦略と言うと、各純戦略にそれを選択する確率を与えたものを指す。「奇数偶数ゲーム」の例では例えば、偶数を60%の確率で奇数を40%の確率で出す、というのがひとつの戦略の例である。ゲーム理論の初期の主要な課題は、標準型ゲームでの戦略と平均的利得の関係の解析であり、利得表がわかっていることが前提であった。
参考文献
- ^ 日本数学会「岩波数学辞典-第3版」岩波書店(1985/12)
- ^ 岡田章「ゲーム理論」有斐閣(1997/01)[要ページ番号]
- ^ 佐々木宏夫「入門ゲーム理論―戦略的思考の科学」日本評論社(2003/03)[要ページ番号]
- ^ 武藤滋夫「ゲーム理論入門」日本経済新聞社(2001/01)[要ページ番号]
関連項目
外部リンク
展開形ゲームと同じ種類の言葉
- 展開形ゲームのページへのリンク
