Information retrieval model
Download as pptx, pdf3 likes3,602 views
情報検索モデル 原著者とアップロード者は別人です。 原著者の許可を得た上でアップロードしています。
![[DL輪読会]Deep Reinforcement Learning that Matters](https://cdn.slidesharecdn.com/ss_thumbnails/deeprlthatmatters-171212050658-thumbnail.jpg?width=560&fit=bounds)
![[GTCJ2018]CuPy -NumPy互換GPUライブラリによるPythonでの高速計算- PFN奥田遼介](https://cdn.slidesharecdn.com/ss_thumbnails/gtcj2018cupypfnryosukeokuta-181009073034-thumbnail.jpg?width=560&fit=bounds)
![[DL輪読会]GLIDE: Guided Language to Image Diffusion for Generation and Editing](https://cdn.slidesharecdn.com/ss_thumbnails/glide2-220107030326-thumbnail.jpg?width=560&fit=bounds)
More Related Content
What's hot (20)
Viewers also liked (20)
![[data analytics showcase] B14: 文字情報の分析基盤 Mroonga by 株式会社インサイトテクノロジー 小幡 一郎](https://cdn.slidesharecdn.com/ss_thumbnails/gewtegxitccqr9e2hb5m-signature-dbdadd8978e07a8eac70e8d97843d87d84136d17cf5a5b684423cc574b8995e4-poli-161007060519-thumbnail.jpg?width=560&fit=bounds)
Similar to Information retrieval model (20)
Information retrieval model
- 1. 情報検索モデル勉強会 D2 加藤 誠
- 2. • 全てのコンテンツが有用とは限りません – 聞きたいときだけ聞いて聞かないときは聞か ないことをお勧めします – 自分の研究と照らし合わせてみてください • 知りたいけどわからない場合は遠慮なく 聞いてください – 完全インタラクティブ制です • スライドでは重要な情報が欠けている場合があり ます 2
- 3. • MSRAに行く前に知識還元を…というか • この話で分かるかもしれないこと 確率モデル Latent Dirichlet Allocation Learning to Rank • できたら同じようなことをしてもらいた いな 3
- 4. 1. 情報検索の基礎 2. 言語モデル I. unigramモデルとクエリ尤度ランキング II. トピックモデル i. Probabilistic Latent Semantic Analysis ii. Latent Dirichlet Allocation 3. 情報検索のための機械学習 I. SVMの基礎 II. Learning to Rank 4. （情報検索の評価手法） 4
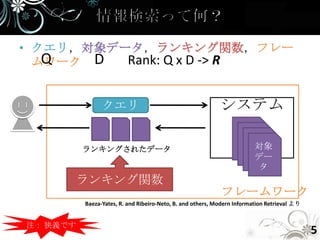
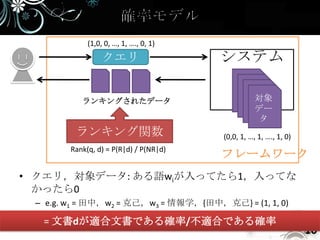
- 5. • クエリ，対象データ，ランキング関数，フレー Q ムワーク D Rank: Q x D -> R クエリ システム ランキングされたデータ 対象 デー タ ランキング関数 フレームワーク Baeza-Yates, R. and Ribeiro-Neto, B. and others, Modern Information Retrieval より 注： 狭義です 5
- 6. • e.g. 「はさんでポンッ」の場合 – クエリ: Q = {(空，君)，(りんご，らっぱ), …} = 語x語 – 対象データ: D = {今日も冷ry, ごりら, …} = 語 – ランキング関数: Rank(q, d) クエリと対象データを引 数にして実数を出す関数 • Rank((空，君), 今ry) = 1000.0 • Rank((空，君), 旭) = -100 高い値＝上位 • Rank((空，君), ごりら) = 10.1 – フレームワーク: 旭君の論文に載っている 6
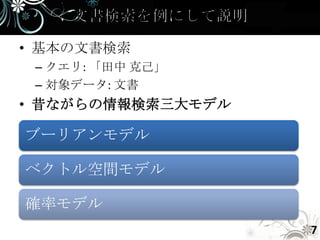
- 7. • 基本の文書検索 – クエリ: 「田中 克己」 – 対象データ: 文書 • 昔ながらの情報検索三大モデル ブーリアンモデル ベクトル空間モデル 確率モデル 7
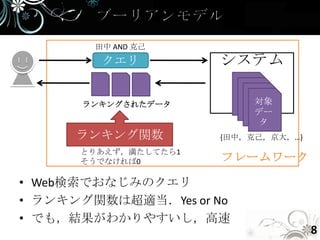
- 8. 田中 AND 克己 クエリ システム ランキングされたデータ 対象 デー タ ランキング関数 {田中，克己，京大，…} とりあえず，満たしてたら1 そうでなければ0 フレームワーク • Web検索でおなじみのクエリ • ランキング関数は超適当．Yes or No • でも，結果がわかりやすいし，高速 8
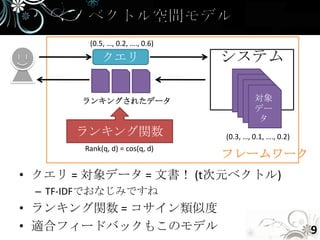
- 9. (0.5, …, 0.2, …., 0.6) クエリ システム ランキングされたデータ 対象 デー タ ランキング関数 (0.3, …, 0.1, …., 0.2) Rank(q, d) = cos(q, d) フレームワーク • クエリ = 対象データ = 文書！ (t次元ベクトル) – TF-IDFでおなじみですね • ランキング関数 = コサイン類似度 • 適合フィードバックもこのモデル 9
- 10. (1,0, 0, …, 1, …., 0, 1) クエリ システム ランキングされたデータ 対象 デー タ ランキング関数 (0,0, 1, …, 1, …., 1, 0) Rank(q, d) = P(R|d) / P(NR|d) フレームワーク • クエリ，対象データ: ある語wiが入ってたら1，入ってな かったら0 – e.g. w1 = 田中，w2 = 克己，w3 = 情報学，{田中，克己} = (1, 1, 0) • ランキング関数 = 文書dが適合文書である確率/不適合である確率 10
- 11. • 袋から玉を取り出す問題 – A，B袋の区別なしに玉を取り出す A袋 B袋 – 「赤」はどっちの袋に入っていた？ • P(A|赤)とP(B|赤)は？ 11
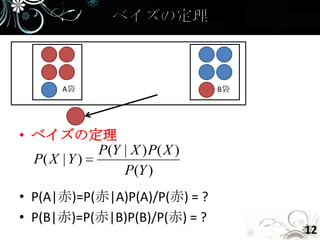
- 12. A袋 B袋 • ベイズの定理 P(Y | X ) P( X ) P( X | Y ) P(Y ) • P(A|赤)=P(赤|A)P(A)/P(赤) = ? • P(B|赤)=P(赤|B)P(B)/P(赤) = ? 12
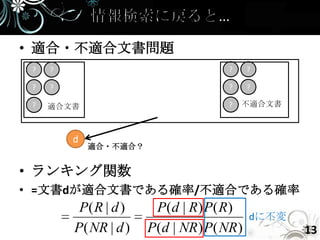
- 13. • 適合・不適合文書問題 ? ? ? ? ? ? ? ? ? 適合文書 ? 不適合文書 d 適合・不適合？ • ランキング関数 • =文書dが適合文書である確率/不適合である確率 P( R | d ) P(d | R) P( R) dに不変 P( NR | d ) P(d | NR ) P( NR ) 13
- 14. • 唯一の手がかり： クエリ=適合文書 ? ? {田中，情報学} ? ? クエリ ? 適合文書 • つまり，P(q|R)は何となく高そう！ • あれ…？ – P(d|R)は？ P({田中，克己}|R)はいくつ？ • 何も分からない… 14
- 15. • 何か仮定が必要です 15
- 16. • 文書は生まれます! (generative model) 1. まず，コインを全語数分用意します • 3語： 「田中」コイン，「克己」コイン，「情報 学」コイン 2. 一枚ずつコイントスします • 表なら使う，裏なら使わない 3. 文書ができました！ （これはBinomial 16
- 17. • {田中，克己}という文書の生成確率は…？ – P({田中，克己}) =P(田中コイン: 表)P(克己コイン: 表) P(情報学コイン: 裏) • 重要な仮定： Naïve Bayse – 語は独立に生成される • そんな馬鹿な！でも一般的な仮定なんです • 数学的に書くと… – d = (1, 1, 0) – P(d) = P(w田中)P(w克己)(1 - P(w情報学)) 17
- 18. • ランキング関数 = 適合文書である確率/不適合である確 率 P( R | d ) P(d | R) ~ P( NR | d ) P(d | NR ) P( w | R) (1 P( w | R)) w d w d P( w | NR) (1 P( w | NR)) w d w d • rw ≡ P(w|R), nw ≡ P(w|NR)として， rw (1 rw ) w d w d rw (1 nw ) (1 rw ) dに不変 nw (1 nw ) w d nw (1 rw ) w (1 nw ) w d w d 18
- 19. • クエリ: {田中, 情報学}の場合 – P(q|R)は高そう • P(田中|R)とP(情報学|R)は高そう • P(田中|NR)とP(情報学|NR)は普通そう – P(田中|NR) = (「田中」を含む文書数) / (全文書数) • P(克己|R)とP(克己|NR)も普通そう (分母=分子．無視) – 文書d:{田中，克己}のランキング関数値は… rw (1 nw ) 0.5(1 df (田中) / N ) Rank(q, d ) w d nw (1 rw ) df (田中) / N (1 0.5) N df (田中) N 1 df (田中) df (田中) idf! 19
- 20. • クエリ，対象データ，ランキング関数，フレー ムワーク • 情報検索三大モデル – ブーリアンモデル 考え方は違うけど結局同じようなことをして – ベクトル空間モデル – 確率モデル • 文書は生成されるという考え – Naïve Bayse ((条件付き)独立性) 20
- 21. 1. 情報検索の基礎 2. 言語モデル I. unigramモデルとクエリ尤度ランキング II. トピックモデル i. Probabilistic Latent Semantic Analysis ii. Latent Dirichlet Allocation 3. 情報検索のための機械学習 I. SVMの基礎 II. Learning to Rank 4. （情報検索の評価手法） 21
- 22. • 文書は生まれます! (今度はサイコ ロ) 1. まず，サイコロを用意します • 3語： 「田中」面，「克己」面，「情報学」面 2. 好きなだけ投げます • 出た目の語を使います 3. 文書ができました！ さっきのコインも言語モデルだと思う(or 言語モデルによる説明) （これはMultinomial Model） 22
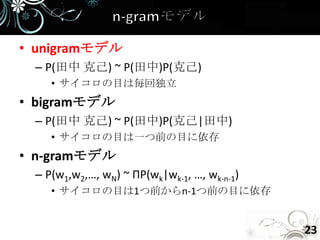
- 23. • unigramモデル – P(田中 克己) ~ P(田中)P(克己) • サイコロの目は毎回独立 • bigramモデル – P(田中 克己) ~ P(田中)P(克己|田中) • サイコロの目は一つ前の目に依存 • n-gramモデル – P(w1,w2,…, wN) ~ ΠP(wk|wk-1, …, wk-n-1) • サイコロの目は1つ前からn-1つ前の目に依存 23
- 24. • コーパス: C = {d1, d2, …, d|C|} • コーパスCの言語モデル – P(w|C) 文書 – 全体用のサイコロ 集合 • 文書diの言語モデル – P(w|di) 文書 di – ある文書di専用のサイコロ 24
- 25. • 文書1: 田中 田中 克己 • 文書2: 田中 情報学 克己 • 文書3: 田中 情報学 情報学 • Q1. P(w|C)を推定せよ • Q2. P(w|di)を推定せよ 25
- 26. • （多値変数の分布の最尤推定） • e.g. – P(田中|C) = 4/9 – P(田中|文書1) = 2/3 26
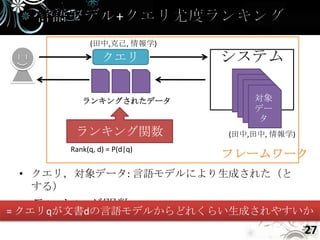
- 27. (田中,克己, 情報学) クエリ システム ランキングされたデータ 対象 デー タ ランキング関数 (田中,田中, 情報学) Rank(q, d) = P(d|q) フレームワーク • クエリ，対象データ: 言語モデルにより生成された（と する） • ランキング関数 = クエリqが文書dの言語モデルからどれくらい生成されやすいか 27
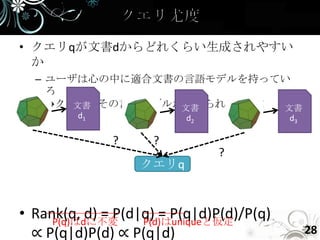
- 28. • クエリqが文書dからどれくらい生成されやすい か – ユーザは心の中に適合文書の言語モデルを持ってい る →クエリはその言語モデルから作られている！ 文書 文書 文書 d1 d2 d3 ? ? ? クエリq • Rank(q, d) = P(d|q) = P(q|d)P(d)/P(q) P(q)はdに不変 P(d)はuniqueと仮定 ∝ P(q|d)P(d) ∝ P(q|d) 28
- 29. • クエリ: 田中 克己 • 文書1: 田中 田中 克己 • 文書2: 田中 情報学 克己 • 文書3: 田中 情報学 情報学 • Q. P(q|d)を推定せよ 29
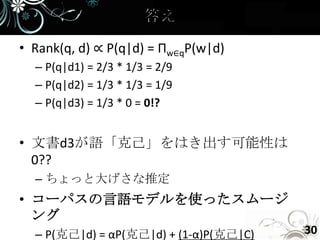
- 30. • Rank(q, d) ∝ P(q|d) = Πw∈qP(w|d) – P(q|d1) = 2/3 * 1/3 = 2/9 – P(q|d2) = 1/3 * 1/3 = 1/9 – P(q|d3) = 1/3 * 0 = 0!? • 文書d3が語「克己」をはき出す可能性は 0?? – ちょっと大げさな推定 • コーパスの言語モデルを使ったスムージ ング – P(克己|d) = αP(克己|d) + (1-α)P(克己|C) 30
- 31. • 文書d1: 田中 データベース • 文書d2: 鈴木 農業 • クエリq: 克己 情報学 • クエリ尤度: P(q|d1) ≒ P(q|d2) ≒ 0!? • 語がマッチしないために検索できない… – クエリ拡張する方法 – ステミングとかNLPしてみる方法 – 語より抽象的なものでマッチング→ トピック モデル 31
- 32. • n-gramモデル – 単語は確率的に生成される • トピックモデル – 単語はトピックから生成される • トピック = 単語の生成分布 トピック Latent Dirichlet Allocation David M. Blei, Andrew Y. Ng, Michael I. Jordan; JMLR, 3(Jan):993-1022, 2003. 32
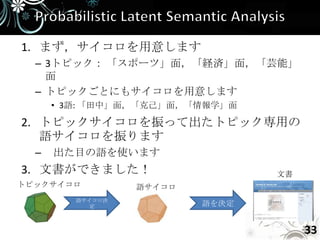
- 33. 1. まず，サイコロを用意します – 3トピック： 「スポーツ」面，「経済」面，「芸能」 面 – トピックごとにもサイコロを用意します • 3語: 「田中」面，「克己」面，「情報学」面 2. トピックサイコロを振って出たトピック専用の 語サイコロを振ります – 出た目の語を使います 3. 文書ができました！ 文書 トピックサイコロ 語サイコロ 語サイコロ決 定 語を決定 33
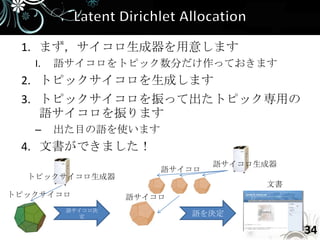
- 34. 1. まず，サイコロ生成器を用意します I. 語サイコロをトピック数分だけ作っておきます 2. トピックサイコロを生成します 3. トピックサイコロを振って出たトピック専用の 語サイコロを振ります – 出た目の語を使います 4. 文書ができました！ 語サイコロ生成器 語サイコロ トピックサイコロ生成器 文書 トピックサイコロ 語サイコロ 語サイコロ決 定 語を決定 34
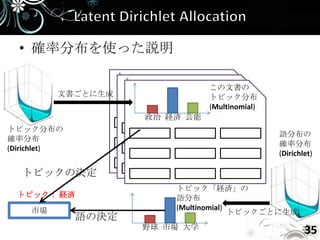
- 35. • 確率分布を使った説明 この文書の 文書ごとに生成 トピック分布 政治 経済 芸能 (Multinomial) 政治 経済 芸能 政治 経済 芸能 トピック分布の 語分布の 確率分布 確率分布 (Dirichlet) (Dirichlet) トピックの決定 トピック「経済」の トピック： 経済 語分布 市場 (Multinomial) トピックごとに生成 語の決定 野球 市場 大学 35
- 36. • PLSAと非常によく似ているが… – トピック・語サイコロにある制約を加えられ る • 1文書に少ない種類のトピックが出るようにする • 1トピックからは少ない種類の語が出るようにする – 学習するパラメータ数が少ない トピックサイコロを文書数分 語サイコロをトピック数分 • PLSA: • LDA: トピックサイコロ生成器 語サイコロ生成器 36
- 37. 注意：ここから難易度が上がりま す 37
- 38. 1. Choose φk ~ Dirichlet(β) 2. For each document di I. Choose θi ~ Dirichlet(α) II. For each word slot wj of di i. Choose zj ~ Multinomial(θi) ii. Choose wj ~ Multinomial(φk) α, β = (0.1, 0.2, 0.3, …): ディリクレ分布のパラメータ φk = (0.1, 0.2, 0.3, …): トピックzkの語分布のパラメー タ ディリクレ分布=サイコロ生 θi = (0.2, 0.3, 0.1, …): 文書diのトピック分布のパラメー 成器 タ 多値分布=サイコロ zi = (0, 0, 0, 1, 0, …): トピック wi = (0, 1, 0, 0, 0, …): 語 38
- 39. • ディリクレ分布 (=多値分布の事前確率) – パラメータ: α = (0.1, 0.2, 0.4, 0.2, 0.1) どのサイコロがでやすい – 変数: θ = (0.2, 0.2, 0.1, 0.2, 0.3) 1 – P( | ) k k 1 Z k • 多値分布 – パラメータ: θ = (0.2, 0.2, 0.1, 0.2, 0.3) どの目がでやすいか – 変数: z = (0, 0, 0, 0, 1)とか(0, 1, 0, 0, 0) zk – P( z | ) k zk 39
- 40. • ベイジアン思想 – 事前分布（確率分布の確率）を入れろー！ • 事前分布のメリット – 1文書に少ない種類のトピックが出るようにす る • α < 1ならこうなる (基本αk = 50/(トピック数)) – 1トピックからは少ない種類の語が出るように する • 同様にβ < 1ならこうなる(基本βj = 0.1, 0.01) – パラメータ数が少ない (α，βのみ) • 過学習しにくくなる – 注： 学習＝α，βの決定．推定＝φ，θの決定 40
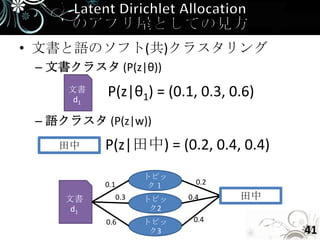
- 41. • 文書と語のソフト(共)クラスタリング – 文書クラスタ (P(z|θ)) 文書 d1 P(z|θ1) = (0.1, 0.3, 0.6) – 語クラスタ (P(z|w)) 田中 P(z|田中) = (0.2, 0.4, 0.4) トピッ 0.1 ク１ 0.2 文書 0.3 トピッ 0.4 田中 d1 ク2 0.6 トピッ 0.4 ク3 41
- 42. • Gibbs Samplingしか知りません… – 他にも変分ベイズがあるらしい • 推定したいもの – θi: 文書iのトピック分布 – φk: トピックkの語分布 • 語にどのトピックが割り当てられている か観測できたらわかるのに… 42
- 43. 1. ランダムにトピックを語に割り当てる 2. For each word in the whole document I. もう一度トピックサイコロを振り直す．た だし， • 他の全ての割り当てが正しいとする • 対象としている語は観測されているとする II. トピックを割り当てる 3. ひたすら2を繰り返す 田中克己 喜連川優 宇多田ヒカル 喜連川優 Mr. Children スピッツ Mr. Children 田中克己 田中克己 田中克己 43
- 44. • もう一度トピックを振り直すときにの確 率 P(zi,j|w, (z-{zi,j})) – 全ての語wと注目している語のトピック以外 同じ語に何回トピックkが のトピックが全てわかっているときにそのト ピックの確率 割り当てられているか？ n (v, k ) v P ( zi , j k | w, (z {zi , j })) (n(i, k ) k) ( n( r , k ) r ) r 同じ文書内で何回トピックk 全体で何回トピックkが が 出ているか？ 割り当てられているか？ 44
- 45. • 言語モデル – ユニグラムモデル – トピックモデル • Probabilistic Latent Semantic Analysis • Latent Dirichlet Allocation • クエリ尤度ランキング 45
- 46. 1. 情報検索の基礎 2. 言語モデル I. unigramモデルとクエリ尤度ランキング II. トピックモデル i. Probabilistic Latent Semantic Analysis ii. Latent Dirichlet Allocation 3. 情報検索のための機械学習 I. SVMの基礎 II. Learning to Rank 4. （情報検索の評価手法） 46
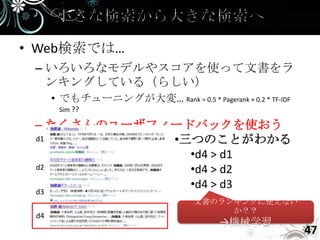
- 47. • Web検索では… – いろいろなモデルやスコアを使って文書をラ ンキングしている（らしい） • でもチューニングが大変… Rank = 0.5 * Pagerank + 0.2 * TF-IDF Sim ?? – たくさんのユーザフィードバックを使おう d1 •三つのことがわかる •d4 > d1 d2 •d4 > d2 •d4 > d3 d3 文書のランキングに使えない か？？ d4 →機械学習 47
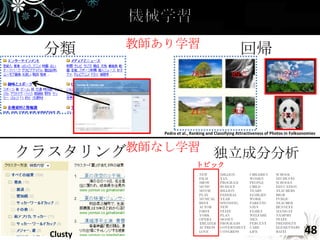
- 48. 分類 教師あり学習 回帰 78点 89点 ??点 21点 31点 ??点 Pedro et al., Ranking and Classifying Attractiveness of Photos in Folksonomies クラスタリング教師なし学習 独立成分分析 トピック Clusty 48
- 49. • 問題： – 訓練データ X = {(x1, y1), (x2, y2), …}が与えられて る • 訓練データはデータxとラベルyのペア – x: k次元ベクトル – y: 離散値(-1, +1)や実数値(21, 89) – テストデータxが与えられた時にそのラベルy は何？ • 例： – スパム判別 • 訓練データ X = {(Page1, スパム), (Page2, スパムじゃない), (Page3, スパム), …} 49
- 50. wTx + b = 0 • 有名な分類モデル wTx + b = +1 wTx + b = -1 • 訓練データ: – X = {((1, 3), +1), ((3, 4), -1), ((4, 9), +1), ((0, 0), -1),} • 分類境界: wTx + b = 0 – wTx + b > +1 なら +1 – wTx + b < -1 なら -1 50
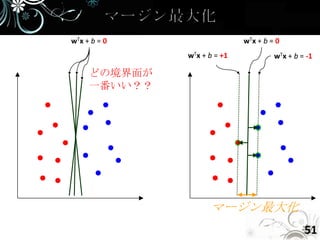
- 51. wTx + b = 0 wTx + b = 0 wTx + b = +1 wTx + b = -1 どの境界面が 一番いい？？ マージン最大化 51
- 52. • 以下の二次計画問題を解くことと等価 2 max マージン最大化 w w T 訓練データは s.t. yi (w x i b) 1 全て正しく分類 • ラグランジュの未定乗数法 n 1 T L ( w , b, a ) w w ai yi w T x i b 1 2 i 1 n w ai y i x i i 1 n 1 n n L' (a) ai ai a j yi y j xT x j i i 1 2i 1 j 1 サポートベクター ai yi (w T x b) 1 0 ai 0 yi (w T x b) 1 52
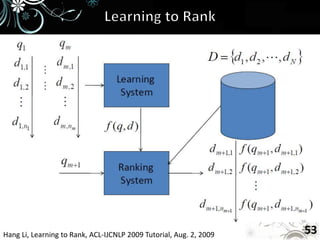
- 53. Hang Li, Learning to Rank, ACL-IJCNLP 2009 Tutorial, Aug. 2, 2009 53
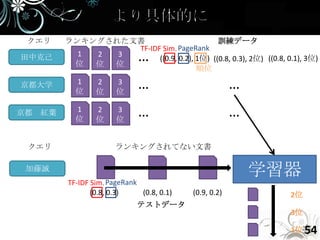
- 54. クエリ ランキングされた文書 訓練データ TF-IDF Sim. PageRank 田中克己 位 1 2 位 位 3 … ((0.9, 0.2), 1位) ((0.8, 0.3), 2位) ((0.8, 0.1), 3位) 順位 京都大学 1 位 2 位 3 位 … … 京都 紅葉 1 位 2 位 3 位 … … クエリ ランキングされてない文書 加藤誠 学習器 TF-IDF Sim. PageRank (0.8, 0.3) (0.8, 0.1) (0.9, 0.2) 2位 テストデータ 3位 1位 54
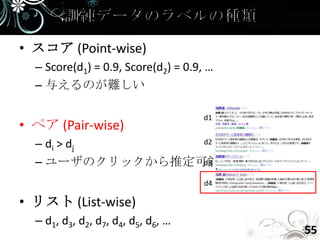
- 55. • スコア (Point-wise) – Score(d1) = 0.9, Score(d2) = 0.9, … – 与えるのが難しい d1 • ペア (Pair-wise) – di > dj d2 – ユーザのクリックから推定可能 d3 d4 • リスト (List-wise) – d1, d3, d2, d7, d4, d5, d6, … 55
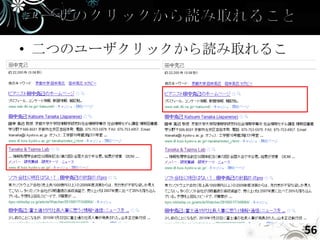
- 56. • 二つのユーザクリックから読み取れるこ とは？ 56
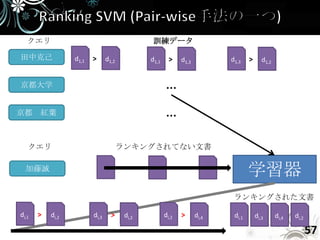
- 57. クエリ 訓練データ 田中克己 d1,1 > d1,2 d1,1 > d1,3 d1,3 > d1,2 京都大学 … 京都 紅葉 … クエリ ランキングされてない文書 加藤誠 学習器 ランキングされた文書 di,1 > di,2 di,3 > di,2 di,2 > di,4 di,1 di,3 di,4 di,2 57
- 58. • SVM 2 max マージン最大化 w w T 訓練データは s.t. yi (w x i b) 1 全て正しく分類 • Ranking SVM 2 max w w T T di > djなら s.t. w xi w xj (di dj) wTxi > wTxj s.t. yi (wT (xi x j ) 0) 0 yi 1 (d i d j ) otherwise 1 58
- 59. • 自分で作る – Rank(q, d) = 0.5 * PageRank(d) + 0.2 * cos(q, d) – Rank(q, d) = 0.3 * PageRank(d) + 0.7 * cos(q, d) – Rank(q, d) = 0.9 * PageRank(d) + 0.1 * cos(q, d) – どれが良いかわからない… • 学習する – Rank(q, d) = w1 * PageRank(d) + w2 * cos(q, d) – 訓練データからw1とw2を決定 59
- 60. • 機械学習とは – 教師あり学習 – 教師なし学習 • SVM – マージン最大化 • Learning to Rank – e.g. Ranking SVM 60
- 61. 1. 情報検索の基礎 2. 言語モデル I. unigramモデルとクエリ尤度ランキング II. トピックモデル i. Probabilistic Latent Semantic Analysis ii. Latent Dirichlet Allocation 3. 情報検索のための機械学習 I. SVMの基礎 II. Learning to Rank 4. （情報検索の評価手法） 61
- 62. • 最初に考えていた「目標」を達成してい るかどうかちゃんと評価できています か？ • 他の論文と同じようなことをしている場 合， 比較していますか？ • 評価はしっかりしてますか？ – ベースライン手法 (簡単なので良い) – 厳密な「正解」の定義 (誰でも正解を作れる か？) 酒井哲也: よりよい検索システム実現のために: 正解の良し悪しを考慮した情報検索評価の動向, 情報処理 Vol.47, No.2, pp.147- 158, 2006 • 複数のユーザ評価のカッパ係数を取って示せるこ 62 酒井哲也: チュートリアル：情報検索テストコレクションと評価指標, 情報処理学会研究報告 2008-FI-89 / 2008-NL-183, pp.1-8,
- 63. • 評価形態 – Intrinsic evaluation • 研究の目的を直接評価 • e.g. 形態素解析の結果を評価 – Extrinsic evaluation • 研究の目的と関係のあるタスクで評価 • e.g. その形態素解析を使って情報検索の精度を評価 – User-oriented evaluation • ユーザを使って評価 • あなたの実験はどれですか？？ Julia R. Galliers and Karen Sparck Jones. 1993. Evaluating natural language processing systems. Technical Report TR-291, Computer Laboratory, University of Cambridge. 63
- 64. • タスク： – 検索意図： 正解となる情報の記述 – クエリ：検索意図を満たす情報を得るための クエリ • 正解データ： – A. 実際のシステムの出力を評価したもの – B. あらかじめ用意した正解 • 適合度判定 – 正解＝「検索意図」を満たすもの！！！ – Not クエリ 64
- 65. Binary Relevance (正解，不正解) Graded Relevance (1, 2, 3, 4, 5) 逆順位 (RR) 重み付き逆順位 正解が一個 正解がたくさん 再現率・適合率・F-measure Normalized Discounted Cumulative Gain (nDCG) 11点平均適合率 平均適合率 (AP) 第r位適合率 65
- 66. • 目的の情報が1つ見つかればよいとき に使う • 正解情報が第r位に現れたとき逆順位 (RR)は タスク1 タスク2 1 正解 RR r 正解 • 全タスクの平均を取って平均逆順位 (MRR)でシステムを評価 K RR=1/2 RR=1 1 1 MRR MRR=3/4 K i 1 ri • とてもブレが大きい – たくさんのタスクを用意しましょう 66
- 67. • 比較的再現率を重視する評 価で有効（らしい） 正解 1/2 • 第r位までの適合率をP(r)と するとAPは 1 L AP I (r ) P(r ) 正解 2/5 Rr1 – ただし，I(r)は第r位が正解の とき1 正解 3/7 R=全正解数，L=システム出力 件数 正解 4/9 • 全タスクの平均を取って MAPでシステムを評価 (よく 全正解数=10なら AP = (1/2+2/5+3/7+4/9)/10 使われる) 67
- 68. • とってもメジャー • Cumulative Gain (CG) – 累積利得（右図参照） L CG( L) g (r ) r 1 • Discounted CG – 1位に正解 > 2位に正解 L g (r ) DCG( L) r 1 log b ( r 1) 酒井哲也: よりよい検索システム実現のために: 正解の良し悪しを考慮した情報検索評価の動向, 情報処理 Vol.47, No.2, pp.147- 68
- 69. • タスクによってDCG 実際の出力 理想の出力 5 の値は大きく変化 4 4 – 簡単/難しいタスク 3 • 正規化 = nDCG 2 – 理想のDCG=1となる 3 ように DCG ( L) nDCG( L) 5 DCG ideal ( L) • nDCG(3), nDCG(5)と 2 かを使う 69
- 70. • α-nDCG – Diversityを考慮したnDCG – トピックごとにnDCGを出すらしい • 順位相関係数 – 適切な順位がわかっているときに利用 – ケンドールの順位相関係数 – スピアマンの順位相関係数 70
- 71. Binary Relevance (正解，不正解) Graded Relevance (1, 2, 3, 4, 5) 逆順位 (RR) 重み付き逆順位 正解が一個 正解がたくさん 再現率・適合率・F-measure Normalized Discounted Cumulative Gain (nDCG) 11点平均適合率 平均適合率 (AP) 第r位適合率 71
- 72. • 長々とすみません • Q&A? • 次の人はだれ？ 72
- 73. • Modern Information Retrieval • Search Engines Information Retrieval in Practice • Introduction to Information Retrieval 73
- 74. • パターン認識と機械学習 上 - ベイズ理論 による統計的予測 • Dr. Hang LiのTutorial – http://research.microsoft.com/en- us/people/hangli/talk.aspx 74
- 75. • Blei et al., Latent dirichlet allocation, JMLR • 酒井哲也氏の解説 – よりよい検索システム実現のために: 正解の 良し悪しを考慮した情報検索評価の動向 – 情報検索テストコレクションと評価指標 75