例えば１次元空間で図１のようなポテンシャルの中の粒子を考えよう。
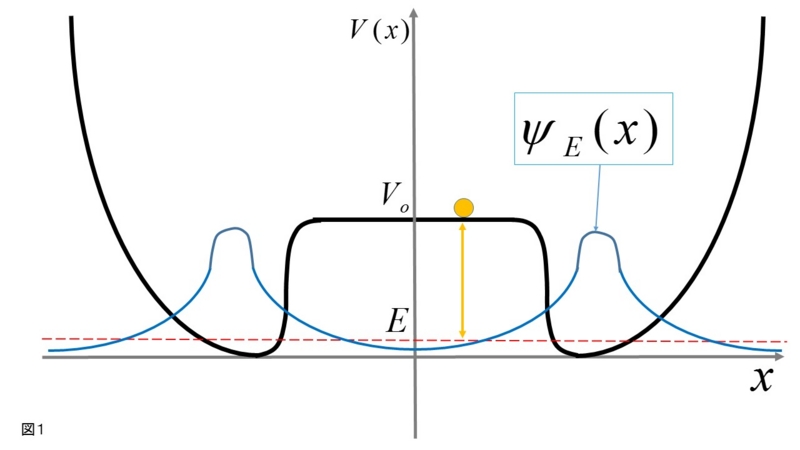
基底状態のエネルギーEは、原点付近のポテンシャルVoより小さい。
しかし、エネルギーが足らないため古典的には粒子の侵入を許さない領域にも、基底状態の波動関数は浸み込んでいる。
「トンネル効果」である。
従って粒子が原点周辺に見つかる確率は、零ではない。
しかし原点付近に粒子が見つかるとすると、その足らなかったエネルギーはどこから来たのか？
それが「問題」である。
測定の結果、例えば図２のように粒子がある点x=ξの周辺に局在した波動関数u(x-ξ)になる。
この状態では明らかにポテンシャルエネルギーの期待値は基底状態のエネルギーより高い。
また粒子がより局在するため、運動エネルギーの期待値も基底状態の時より高くなる。
従って確かに粒子はエネルギーの高い状態に見つかったことになる。
他の地点に見つかる可能性も考慮しても、あらゆる測定結果に対して平均化した測定後状態のエネルギーの期待値はEより高いことも分かる。
ではトンネル効果においてエネルギー保存則が破れているのか。
これは有り得ない。
量子力学でもエネルギー保存則は厳密に成り立っているのである。
（量子力学で、短時間の間でもエネルギー保存則が成り立つことについては、以下の記事を参照。
http://mhotta.hatenablog.com/entry/2014/03/11/155744
http://mhotta.hatenablog.com/entry/2014/04/26/061840 ）
答えは、「測定機から粒子にエネルギーが流れ込んだ。」である。
測定をしたければ、その測定機もエネルギーを持つ１つの物理系として用意する必要がある。
そして測定による状態変化のために測定される粒子のエネルギーが増えるならば、その測定機がそのエネルギーを与える必要があるのだ。
測定で得る情報の代償として、測定機のエネルギー消費が起こるわけだ。
もし測定機が必要なエネルギーを持っていなければ、その測定機が正確に測定を実行することはない。
つまりこの議論は、位置測定を実行できる測定機の駆動エネルギー下限を与える。
これはトンネル効果に限った話ではない。
位置測定に関する量子力学の一般的性質である。
具体的に位置測定の１つの例を挙げてみよう。
粒子が運動するx軸と直交するｙ軸を考える。
（粒子は外場によってｘ軸の直線上に閉じ込められているとする。）
図３のように、ｙ軸の正方向に伝搬する局在した光パルスを各ｘの値毎に放つと、ある地点のパルスだけ散乱し、他のパルスは何事もなかったように通過する。
パルスをｙ軸の正の領域にあるスクリーンで捕らえれば、粒子がｘ軸上のどこの地点にいたのがパルスの横幅程度で分かる。
粒子は測定前に固有値Eを持っていたが、パルスとの散乱後には測定の効果としてそれより高いエネルギー期待値E(f)を持つ。
粒子を捕まえたパルスの散乱後のエネルギー期待値E(f;γ)は、散乱前のエネルギー期待値E(i;γ)より小さくなる。
そしてその差が粒子が得たエネルギーE(f)-Eに一致するのだ。
測定で得られる情報量とその代償としてのエネルギー消費が絡み合うこのような現象は、量子エンタングルメントを持った量子多体系の基底状態においても顕著に現れる。
基底状態は、定義により最低エネルギー状態である。
しかし部分系の物理量の測定をして有意な情報を得たとすると、基底状態のエンタングルメントはこの測定行為によって破壊され、測定後状態は基底状態とは異なる励起状態に成らざるを得ない。
つまり基底状態にある量子系から一定の情報量を取り出すには、必ずその系にエネルギーを与える必要がある。
このエンタングルした基底状態における「情報量とエネルギーの間のトレードオフ関係」は、量子エネルギーテレポーテーション（Quantum Energy Teleportation, QET）という新しい量子プロトコルとも深く関連している。
このQETについては機会を改めて紹介しよう。
