本稿ã§ã¯ Even GPT-5.2 Can't Count to Five: The Case for Zero-Error Horizons in Trustworthy LLMs ã‚’ã‚‚ã¨ã«ã€æœ€å…ˆç«¯ã® LLM ãŒæœªã ã«ã”ãç°¡å˜ãªå•é¡Œã§ã™ã‚‰ãƒŸã‚¹ã™ã‚‹ã“ã¨ã‚’è°è«–ã—ã¾ã™ã€‚
具体例ã¨ã—ã¦ã¯ã€11000 ã«å«ã¾ã‚Œã‚‹ 1 ã®æ•°ãŒå¶æ•°ã‹å¥‡æ•°ã‹èžãã¨ã€gpt-5.2-2025-12-11 ã¯å¥‡æ•°ã¨ç”ãˆã¾ã™ã€‚ã¾ãŸã€((((()))))) ã®ã‚«ãƒƒã‚³ã®ãƒãƒ©ãƒ³ã‚¹ãŒå–ã‚Œã¦ã„ã‚‹ã‹èžãã¨ã€å–ã‚Œã¦ã„ã‚‹ã¨ç”ãˆã¾ã™ã€‚127×82 を計算ã•ã›ã‚‹ã¨ã€10314 ã¨ç”ãˆã¾ã™ï¼ˆæ£è§£ã¯ 10414)。ã“ã®ã“ã¨ã¯ä»¥ä¸‹ã®ã‚³ãƒžãƒ³ãƒ‰ã§ç¢ºèªã§ãã¾ã™ã€‚
ã“れら㯠API ã‚ー $OPENAI_API_KEY ã•ãˆè¨å®šã™ã‚Œã°ã‚³ãƒ”ペã§èª°ã§ã‚‚試ã›ã‚‹ã®ã§ãœã²è©¦ã—ã¦ã¿ã¦ãã ã•ã„ã。
GPT-5.2 ã¯æµä½“力å¦ã®è¤‡é›‘ãªã‚·ãƒŸãƒ¥ãƒ¬ãƒ¼ã‚·ãƒ§ãƒ³ã‚’è¡Œã„ã€ã‚¢ã‚»ãƒ³ãƒ–リ言語ã®ãƒ‹ãƒƒãƒãªæœ€é©åŒ–テクニックを駆使ã—ã¦ä½Žãƒ¬ã‚¤ãƒ¤ãƒ¼ãƒ—ãƒã‚°ãƒ©ãƒŸãƒ³ã‚°ã‚’ã“ãªã™ã“ã¨ãŒã§ãã¾ã™ã€‚ã‚‚ã¯ã‚„人間ã®èƒ½åŠ›ã‚’上回ã£ãŸã‹ã«è¦‹ãˆã¾ã™ãŒã€æœªã ã«äººé–“ã‹ã‚‰ã™ã‚‹ã¨è€ƒãˆã‚‰ã‚Œãªã„よã†ãªæ„šã‹ãªãƒŸã‚¹ã‚’犯ã™ã“ã¨ãŒã‚ã‚Šã¾ã™ã€‚ã“ã®ã‚ˆã†ãªèƒ½åŠ›ã®ã¡ãã¯ãã•ãŒä¿¡é ¼æ€§ã®é«˜ã„é ˜åŸŸã« LLM を展開ã™ã‚‹ã¨ãã®èª²é¡Œã«ãªã£ã¦ã„ã¾ã™ï¼ˆãã—ã¦ã“ã®ã¡ãã¯ãã•ã®ãŠã‹ã’ã§äººé–“ã¯ã¾ã LLM ã«å®Œå…¨ã«ä»•äº‹ã‚’奪ã‚ã‚Œã¦ã„ã¾ã›ã‚“。)大è¦æ¨¡ãªé‡‘èžå–引をã™ã‚‹ AI ãŒã€é«˜åº¦ãªé‡‘èžç†è«–を駆使ã—ãŸã‚ã¨ã§ã€127×82 を計算ミスã—ã¦å¤§æを被ã£ãŸã‚‰ã©ã†ã§ã—ょã†ã‹ã€‚原å炉をå¸ã‚‹ AI ãŒçŠ¶æ…‹ãƒ•ãƒ©ã‚° 11000 ã« 1 ãŒå¥‡æ•°å€‹ç«‹ã£ã¦ã„ã‚‹ã¨è€ƒãˆã¦å‹•ä½œä¸ã®åŽŸå炉ã®æ‰‰ã‚’é–‹ã„ã¦ã—ã¾ã£ãŸã‚‰ã©ã†ã§ã—ょã†ã‹ã€‚目も当ã¦ã‚‰ã‚Œã¾ã›ã‚“。
ã“ã®è«–æ–‡ã§ã¯ã€ã“ã®èƒ½åŠ›ã®ã€Œç©´ã€ã‚’評価ã™ã‚‹ãŸã‚ã«ã‚¼ãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œ (Zero-Error Horizon; ZEH) ã¨ã„ã†æŒ‡æ¨™ã‚’æ案ã—ã¦ã„ã¾ã™ã€‚
モデルã€ã‚¿ã‚¹ã‚¯ã€ãƒ—ãƒãƒ³ãƒ—トã€ä¹±æ•°ã‚’固定ã—ã¾ã™ã€‚例ãˆã°ãƒ¢ãƒ‡ãƒ«ã¯ gpt-5.2-2025-12-11 ã€ã‚¿ã‚¹ã‚¯ã¯æŽ›ã‘ç®—ã€ãƒ—ãƒãƒ³ãƒ—ト㯠{"instructions": "Answer with only the integer.", "input": "{a}*{b}="} ã§ã™ã€‚å•é¡Œã‚µã‚¤ã‚ºã®å°ã•ã„é †ã«ã™ã¹ã¦ã®å•é¡Œä¾‹ã‚’入力ã—ãŸã¨ãã€ã‚µã‚¤ã‚º n ã¾ã§ã¯å…¨ã¦æ£è§£ã™ã‚‹ãŒã€ã‚µã‚¤ã‚º n + 1 ã§å¤±æ•—ã™ã‚‹å•é¡ŒãŒã‚ã‚‹ã¨ãã€ã‚¼ãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã¯ n ã§ã‚ã‚‹ã¨ã—ã¾ã™ã€‚é–“é•ãˆãŸã‚µã‚¤ã‚º n + 1 ã®å•é¡Œä¾‹ã‚’リミッター (ZEH limiter) ã¨å‘¼ã³ã¾ã™ã€‚ゼãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã¨ãƒªãƒŸãƒƒã‚¿ãƒ¼ã¯åŸºæœ¬çš„ã«ã¯å…¨æŽ¢ç´¢ã§æ±‚ã‚ã¾ã™ï¼ˆè«–æ–‡ã§ã¯å°‘ã—高速化ã™ã‚‹æ–¹æ³•ã«ã¤ã„ã¦ã‚‚è¿°ã¹ã¦ã„ã¾ã™ï¼‰ã€‚
例ãˆã°ã€å•é¡Œã‚µã‚¤ã‚ºã‚’ a 㨠b ã®å¤§ãã„æ–¹ã®å€¤ã¨ã™ã‚‹ã¨ã€gpt-5.2-2025-12-11 㯠126 ã¾ã§ã®æŽ›ã‘算(計 126×126 = 15876å•ï¼‰ ã«ã¯å…¨ã¦æ£è§£ã—ã¾ã™ãŒã€127×82 ã§é–“é•ãˆã‚‹ã®ã§ã€ã‚¼ãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã¯ 126ã€ãƒªãƒŸãƒƒã‚¿ãƒ¼ã¯ 127×82 ã§ã™ã€‚
å•é¡Œã‚µã‚¤ã‚ºã‚’æ–‡å—列長ã¨ã™ã‚‹ã¨ã€gpt-5.2-2025-12-11 㯠4 æ–‡å—ã¾ã§ã® 01 æ–‡å—列(計 24 = 16 å•ï¼‰ã«ã¤ã„ã¦ã¯ 1 ã®æ•°ã®å¶å¥‡ã«å…¨ã¦æ£è§£ã—ã¾ã™ãŒã€11000 ã§é–“é•ãˆã‚‹ã®ã§ã‚¼ãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã¯ 4ã€ãƒªãƒŸãƒƒã‚¿ãƒ¼ã¯ 11000 ã§ã™ã€‚
ã¾ãŸã€gpt-5.2-2025-12-11 㯠10 æ–‡å—ã¾ã§ã®ã‚«ãƒƒã‚³åˆ—(計 210 = 1024å•ï¼‰ã«ã¤ã„ã¦ãƒãƒ©ãƒ³ã‚¹ãŒå–ã‚Œã¦ã„ã‚‹ã‹ã‚’å…¨å•æ£è§£ã—ã¾ã™ãŒã€((((()))))) ã§é–“é•ãˆã‚‹ã®ã§ã‚¼ãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã¯ 10ã€ãƒªãƒŸãƒƒã‚¿ãƒ¼ã¯ ((((()))))) ã§ã™ã€‚
ゼãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã§ã¯ãƒ—ãƒãƒ³ãƒ—ト(文脈)ã¨ä¹±æ•°ã¯å›ºå®šã—ã¦ã„ã‚‹ã“ã¨ã«æ³¨æ„ã—ã¦ãã ã•ã„。プãƒãƒ³ãƒ—トや乱数を変ãˆã‚‹ã¨æ£è§£ã™ã‚‹ã“ã¨ã‚‚ã‚ã‚‹ã§ã—ょã†ã€‚ウェブ上㮠ChatGPT ã¯ã€API 経由ã®å ´åˆã¨ã¯ä¹±æ•°ã‚„プãƒãƒ³ãƒ—トãŒé•ã„ã¾ã™ã‹ã‚‰ã€11000 ã«ã¤ã„ã¦æ£è§£ã™ã‚‹ã‹ã‚‚ã—ã‚Œã¾ã›ã‚“。ã—ã‹ã—ã€ãƒ—ãƒãƒ³ãƒ—トや乱数次第ã§ç°¡å˜ãªå•é¡Œã§ã‚‚é–“é•ã„ã†ã‚‹ã¨ã„ã†ã“ã¨ãŒé‡è¦ã§ã™ã€‚ãƒã‚¤ãƒªã‚¹ã‚¯ãªé ˜åŸŸã§ã¯ã€100 回㫠1 回ã§ã‚‚é–“é•ãˆã¦ã—ã¾ã†ã®ã§ã¯å¤§å•é¡Œã§ã™ã€‚ã¾ãŸã€ãƒªãƒŸãƒƒã‚¿ãƒ¼ã®ä¸ã«ã¯ãƒ—ãƒãƒ³ãƒ—トや乱数ã®å¤‰åŒ–ã«å¯¾ã—ã¦æ¯”è¼ƒçš„é ‘å¥ãªã‚‚ã®ã‚‚å˜åœ¨ã—ã¾ã™ã€‚((((()))))) ãŒãã®ä¾‹ã§ã™ã€‚((((()))))) ã¯ãƒãƒ©ãƒ³ã‚¹ã—ã¦ã„る? ã¨ã‚¦ã‚§ãƒ–ã® ChatGPT ã«èžãã¨ãã‚Œãªã‚Šã®ç¢ºçŽ‡ï¼ˆ50% ãらã„ã§ã—ょã†ã‹ï¼‰ã§ãƒãƒ©ãƒ³ã‚¹ã—ã¦ã„ã‚‹ã¨ç”ãˆã‚‹ã“ã¨ãŒã‚ã‹ã‚Šã¾ã—ãŸã€‚GPT-5.2-Thinking ã®ã‚ˆã†ã«æ€è€ƒã®é€£éŽ– (Chain-of-Thought) を許å¯ã—ã¦ã‚‚ミスã—ã¾ã™ã€‚GPT-5.2 ã¯æœ¬è³ªçš„ã«ã“ã®å•é¡ŒãŒè‹¦æ‰‹ãªã‚ˆã†ã§ã™ã€‚ãœã²è‰²ã‚“ãªãƒ¢ãƒ‡ãƒ«ã‚„プãƒãƒ³ãƒ—トã§è©¦ã—ã¦ã¿ã¦ãã ã•ã„ã。

ã‚ã–ã‚ã–掛ã‘算やカッコã®å¯¾å¿œã‚’ LLM ã«è§£ã‹ã›ãªã„ã ã‚ã†ã¨æ€ã†æ–¹ã‚‚ã„ã‚‹ã‹ã‚‚ã—ã‚Œã¾ã›ã‚“ãŒã€ã“ã®ã‚ˆã†ãªåŸºæœ¬çš„ãªå•é¡Œã¯è¤‡é›‘ãªå•é¡Œã®ã‚µãƒ–タスクã¨ã—ã¦ç™»å ´ã™ã‚‹ã“ã¨ãŒã‚ã‚Šã¾ã™ã€‚複雑ãªæ•°å¦ã®å•é¡Œã‚’æ€è€ƒã®é€£éŽ–ã§è§£ãã¨ãã€é€”ä¸å¼ã§æŽ›ã‘ç®—ãŒå‡ºã¦ãã‚‹ã“ã¨ãŒã‚ã‚Šã¾ã™ã€‚ã“ã“ã§ãƒŸã‚¹ã‚’ã™ã‚‹ã¨ãã®ãƒŸã‚¹ãŒä¼æ’ã—ã¦æœ€çµ‚çµè«–ãŒé–“é•ã†ã‹ã‚‚ã—ã‚Œã¾ã›ã‚“。電å“ã‚„ Python プãƒã‚°ãƒ©ãƒ を呼ã³å‡ºã›ã°ã‚ˆã„ã‹ã‚‚ã—ã‚Œã¾ã›ã‚“ãŒã€ã“ã®ã‚ˆã†ãªå˜ç´”ãªã‚µãƒ–タスクã§ã™ã‚‰æ¯Žå›žãƒ„ールを呼ã³å‡ºã™ã®ã¯å¤§å¤‰ã§ã™ã—ã€ãƒ„ール呼ã³å‡ºã—ã‚’ã™ã‚‹ã¹ãã‹ã®åˆ¤æ–をミスã™ã‚‹ã“ã¨ã‚‚ã‚ã‚Šã¾ã™ã€‚実際ã€GPT-5.2-Thinking ã¯ãƒ„ール呼ã³å‡ºã—を許å¯ã•ã‚Œã¦ã„ã‚‹ã«ã‚‚ã‹ã‹ã‚らãšã€å‘¼ã³å‡ºã•ãšã« ((((()))))) ã®ã‚«ãƒƒã‚³ã‚’自分ã§æ•°ãˆã¦ãƒŸã‚¹ã—ã¦ã—ã¾ã£ã¦ã„ã¾ã™ã€‚
ゼãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã¯ã€ã“ã®ã‚ˆã†ãª LLM ã®èƒ½åŠ›ã®ã¡ãã¯ãã•ã‚„「穴ã€ã‚’効果的ã«åˆ¤å®šã§ãã¾ã™ã€‚ã¾ãŸã€æ¬¡ã®ã‚ˆã†ãªæ•°å¤šãã®ãƒ¡ãƒªãƒƒãƒˆãŒã‚ã‚Šã¾ã™ã€‚
リミッターãŒç¢ºå›ºã¨ã—ãŸè¨¼æ‹ ã«ãªã‚‹
ゼãƒã‚¨ãƒ©ãƒ¼å¢ƒç•ŒãŒ n 以下ã§ã‚ã‚‹ã“ã¨ã¯ä¸Šã«æŽ²è¼‰ã—ãŸã‚³ãƒžãƒ³ãƒ‰ã‚’実行ã™ã‚Œã°èª°ã§ã‚‚一発ã§æ¤œè¨¼ã§ãã¾ã™ã€‚実際ã«ã‚³ãƒžãƒ³ãƒ‰ã‚’実行ã—ã¦å‡ºåŠ›ã‚’見れ㰠GPT-5.2 ãŒã“れらã®å•é¡Œã§ãƒŸã‚¹ã™ã‚‹ã“ã¨ã¯ç«ã‚’見るよりも明らã‹ã§ã‚ã‚Šã€èª°ã§ã‚ã‚Œãƒãƒƒã‚リç´å¾—ã•ã›ã‚‹ã“ã¨ãŒã§ãã¾ã™ã€‚ã“ã‚Œã¯æ•°å¦çš„ã«ã‚‚コミュニケーションã®ä¸Šã§ã‚‚好ã¾ã—ã„ã§ã™ã€‚
自動的ã«é©šãã®ã‚ã‚‹çµæžœãŒå¾—られる
GPT-5.2 ㌠11000 ã® 1 ã®æ•°ã‚’カウントã§ããªã„ã€((((()))))) ãŒãƒãƒ©ãƒ³ã‚¹ã—ã¦ã„ã‚‹ã‹åˆ†ã‹ã‚‰ãªã„ã€ã¨ã„ã†çµæžœã¯é©šãã§ã‚り示唆ã«å¯Œã¿ã¾ã™ã€‚ã“れらã®ãƒªãƒŸãƒƒã‚¿ãƒ¼ã¯ã‚¼ãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã‚’評価ã™ã‚‹ã¨è‡ªå‹•çš„ã«å‰¯ç”£ç‰©ã¨ã—ã¦å¾—られã¾ã™ã€‚((((()))))) ã¯ã€Œãã‚Œã£ã½ã„ã€ä¾‹ã§ã™ãŒã€è©¦è¡ŒéŒ¯èª¤ã§æŽ¢ã—ãŸã‚ã‘ã§ã¯ãªãã€æœ€ã‚‚å°ã•ã„é–“é•ã„を自動ã§è©•ä¾¡ã—ãŸçµæžœç™ºè¦‹ã—ã¾ã—ãŸã€‚ã“れら㯠GPT-5.2 ãŒé–“é•ãˆã‚‹å•é¡Œã®ä¸ã§æœ€ã‚‚å°ã•ã„ç°¡å˜ãªä¾‹ãªã®ã§ã€ãã‚“ãªã«ç°¡å˜ãªä¾‹ã§ã‚‚é–“é•ãˆã‚‹ã¨ã„ã†ç‚¹ã§æœ€å¤§ç´šã®æ´žå¯Ÿã¨é©šããŒå¾—られã¾ã™ã€‚
ã“ã®ã“ã¨ã¯æ•µå¯¾çš„例 (adversarial example) ã¨ä¼¼ã¦ã„ã¾ã™ãŒã€å®Ÿéš›ä¸Šã®æ„義ã¯ç•°ãªã‚Šã¾ã™ã€‚ 敵対的例ã¯ä¸è‡ªç„¶ã§ã€åˆ†å¸ƒå¤–ã®ä¾‹ãªã®ã§ãƒ¢ãƒ‡ãƒ«ãŒé–“é•ã†ã®ã¯ã‚ã‚‹æ„味当然ã§ã™ï¼ˆã‚€ã—ã‚é–“é•ã†æ–¹ãŒæ£ã—ã„ã¨ã‚‚言ãˆã¾ã™ã€‚詳ã—ã㯠人間には認知できない情報を活用するAIたち - ジョイジョイジョイ ã‚’èªã‚“ã§ã¿ã¦ãã ã•ã„ã)。一方ã€ãƒªãƒŸãƒƒã‚¿ãƒ¼ã¯è‡ªç„¶ã§ã€æ™®é€šã«èµ·ã“ã‚Šã†ã‚‹ä¾‹ã§ã‚ã‚‹ã«ã‚‚ã‹ã‹ã‚らãšã€ãã—ã¦ã“ã“ã¾ã§å°ã•ãªç°¡å˜ãªä¾‹ã§ã‚ã‚‹ã«ã‚‚ã‹ã‹ã‚らãšãƒ¢ãƒ‡ãƒ«ãŒãƒŸã‚¹ã‚’ã™ã‚‹ã¨ã„ã†ç‚¹ã§ã€å®Ÿéš›ä¸Šã®æ„義ã¨é©šããŒã‚ã‚Šã¾ã™ã€‚
æ£è§£çŽ‡ã«ã¯ã‚¹ã‚±ãƒ¼ãƒ«ã®æ£æ„性ãŒã‚ã‚‹ãŒã‚¼ãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã«ã¯ãªã„
æ£è§£çŽ‡ (accuracy) ã¯æœ€ã‚‚よã使ã‚れる評価指標ã§ã™ãŒã€æ£è§£çŽ‡ã‚’評価ã™ã‚‹ãŸã‚ã«å•é¡Œã®ç¯„囲を人間ã®è©•ä¾¡è€…ãŒã‚らã‹ã˜ã‚定ã‚ãªãã¦ã¯ãªã‚Šã¾ã›ã‚“。例ãˆã°æŽ›ã‘ç®—ã®æ£è§£çŽ‡ã‚’求ã‚ã‚‹ã¨ãã€1×1 ã‹ã‚‰ 99×99 ã®å•é¡Œã®ç¯„囲ã®æ£è§£çŽ‡ã‚’評価ã™ã‚‹ã€ãªã©ã¨å®šã‚ã¾ã™ã€‚ã—ã‹ã—ã€ã“ã®ç¯„囲ã®è¨å®šãŒã€å…ˆå…¥è¦³ã«å·¦å³ã•ã‚Œã‚‹ã“ã¨ãŒã‚ã‚Šã€ã¾ãŸè©•ä¾¡è€…ãŒè‡ªèº«ã®æ‰‹æ³•ã‚’良ã見ã›ã‚‹ãŸã‚ã®æ“作ã®å¯¾è±¡ã«ãªã‚‹ã“ã¨ã‚‚ã‚ã‚Šã¾ã™ã€‚以下ã®å›³ã¯ Qwen2.5-7B-Instruct 㨠Qwen2.5-72B-Instruct ã®æŽ›ã‘ç®—ã®è©•ä¾¡çµæžœã§ã™ã€‚
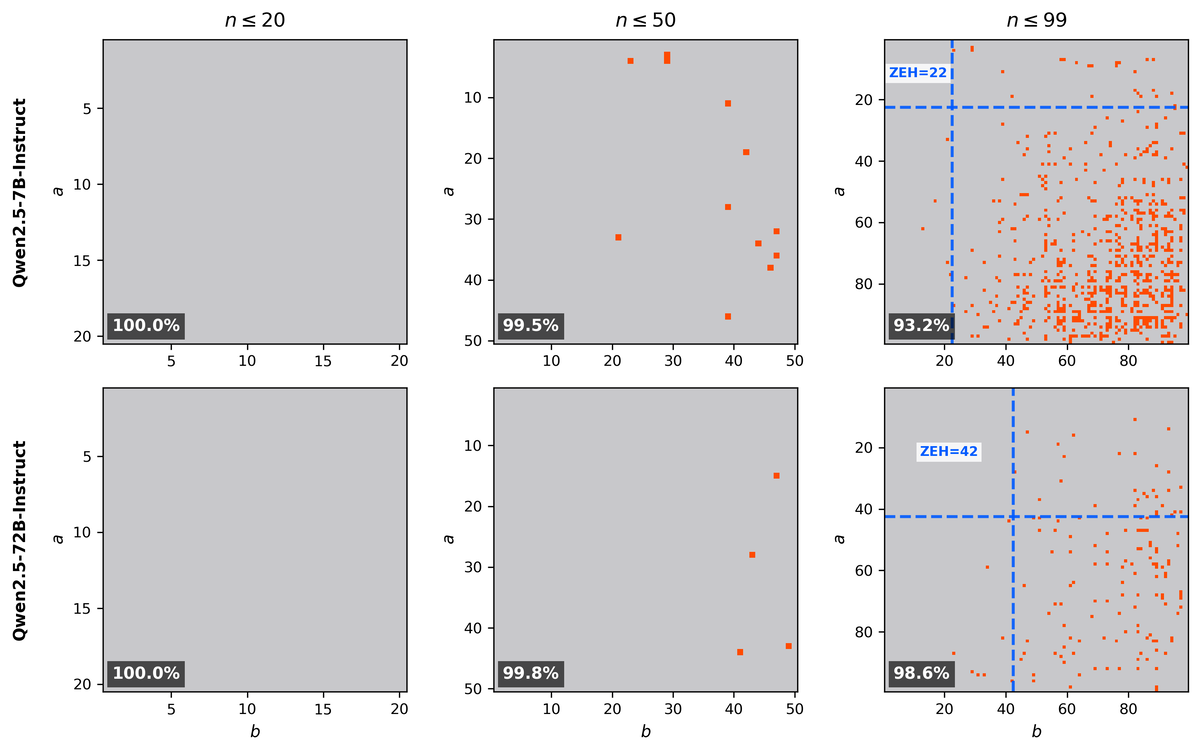
72B モデルを 7B モデルã«åœ§ç¸®ã™ã‚‹ã“ã¨ã‚’æ案ã™ã‚‹äººã¯ã€å·¦ã®å›³ã‚„真んä¸ã®å›³ã‚’見ã›ã¦ã€ã€Œ72B モデルを 7B モデル㫠10 å€ä»¥ä¸Šåœ§ç¸®ã—ã¦ã‚‚精度ã¯ã»ã¨ã‚“ã©è½ã¡ãªã‹ã£ãŸã€ã¨ä¸»å¼µã™ã‚‹ã‹ã‚‚ã—ã‚Œã¾ã›ã‚“。ã“ã‚Œã«é¨™ã•ã‚Œã‚‹èªè€…ã‚‚ã„ã‚‹ã§ã—ょã†ã€‚ã—ã‹ã—ã€å³ã®å›³ã®ã‚ˆã†ã«åˆ¥ã®ãƒ¬ãƒ³ã‚¸ã§è©•ä¾¡ã™ã‚‹ã¨ã€å…¨ã別ã®å‚¾å‘ã«ãªã‚Šã¾ã™ã€‚ã“ã®ã‚ˆã†ã«ã€å•é¡Œã®ç¯„囲次第ã§çµæžœã¯å¤§ãã変化ã—ã¾ã™ãŒã€è©•ä¾¡è€…ã®å…ˆå…¥è¦³ã‚„æ£æ„ã§ç¯„囲を決定ã™ã‚‹ãŸã‚ã«ã€è©•ä¾¡ã«ãƒã‚¤ã‚¢ã‚¹ãŒå…¥ã‚Šè¾¼ã‚€ã“ã¨ãŒã‚ã‚Šã¾ã™ã€‚
一方ã€ã‚¼ãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã¯ãƒ¢ãƒ‡ãƒ«è‡ªèº«ãŒå®šã‚ã¾ã™ã€‚人間ãŒæ£æ„çš„ã«è©•ä¾¡ç¯„囲を決ã‚る余地ã¯ã‚ã‚Šã¾ã›ã‚“。ã“ã®ãŸã‚ã€22 vs 42 ã¨ã„ã†ã‚ˆã†ã«ã€ç¯„囲ã®è¨å®šã«å·¦å³ã•ã‚Œãªã„客観的ãªå€¤ãŒå¾—られã¾ã™ã€‚
å•é¡Œã®ç¯„囲 = 難度をã‚らã‹ã˜ã‚固定ã›ãšã«ãƒ¢ãƒ‡ãƒ«è‡ªä½“ã«æ±ºå®šã•ã›ã‚‹ã¨ã„ã†ã®ãŒã‚¼ãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã®å¤§ããªç‰¹å¾´ã§ã™ã€‚
指標ã¨ã—ã¦æ™‚代é…ã‚Œã«ãªã‚Šã¥ã‚‰ã„
範囲をã‚らã‹ã˜ã‚固定ã™ã‚‹ãƒ™ãƒ³ãƒãƒžãƒ¼ã‚¯ã¯æ™‚代é…ã‚Œã«ãªã‚Šã¾ã™ã€‚1×1 ã‹ã‚‰ 50×50 ã¾ã§ã® 2500 å•ã‹ã‚‰ãªã‚‹ãƒ™ãƒ³ãƒãƒžãƒ¼ã‚¯ã¯ 7B ã‚„ 72B モデルã®èƒ½åŠ›ã‚’ã»ã¨ã‚“ã©è¦‹åˆ†ã‘られã¾ã›ã‚“。99×99 ã®ãƒ™ãƒ³ãƒãƒžãƒ¼ã‚¯ã¯è¦‹åˆ†ã‘られã¦ã„ã¾ã™ãŒã€ã„ãšã‚Œé£½å’Œã™ã‚‹ã§ã—ょã†ã€‚MNIST ã‚‚ CIFAR-10 ã‚‚ GLUE ã‚‚ã€åŒã˜é‹å‘½ã‚’辿ã£ã¦ãã¾ã—ãŸã€‚
一方ã€ã‚¼ãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã¯é›£åº¦ã‚’ã‚らã‹ã˜ã‚固定ã›ãšã€ãƒ¢ãƒ‡ãƒ«ã®èƒ½åŠ›ã«ã‚ã‚ã›ã¦ã‚ªãƒ¼ãƒ—ンエンドã«é›£åº¦ãŒè¨å®šã•ã‚Œã‚‹ã®ã§ã€æ™‚代é…ã‚Œã«ãªã‚Šã¥ã‚‰ã„ã§ã™ã€‚
æ§‹é€ çš„ãªã‚¨ãƒ©ãƒ¼ãƒ‘ターンを優é‡ã§ãã‚‹
æ£è§£æ•°ãŒåŒã˜ãƒ¢ãƒ‡ãƒ«ã§ã‚‚ã€é–“é•ã„æ–¹ã®ãƒ‘ターンã¯æ§˜ã€…ã§ã™ã€‚以下ã¯ã©ã¡ã‚‰ã‚‚æ£è§£çŽ‡ãŒ 90% ã®ãƒ‘ターンã§ã™ãŒã€æ§‹é€ ãŒå…¨ãé•ã„ã¾ã™ã€‚
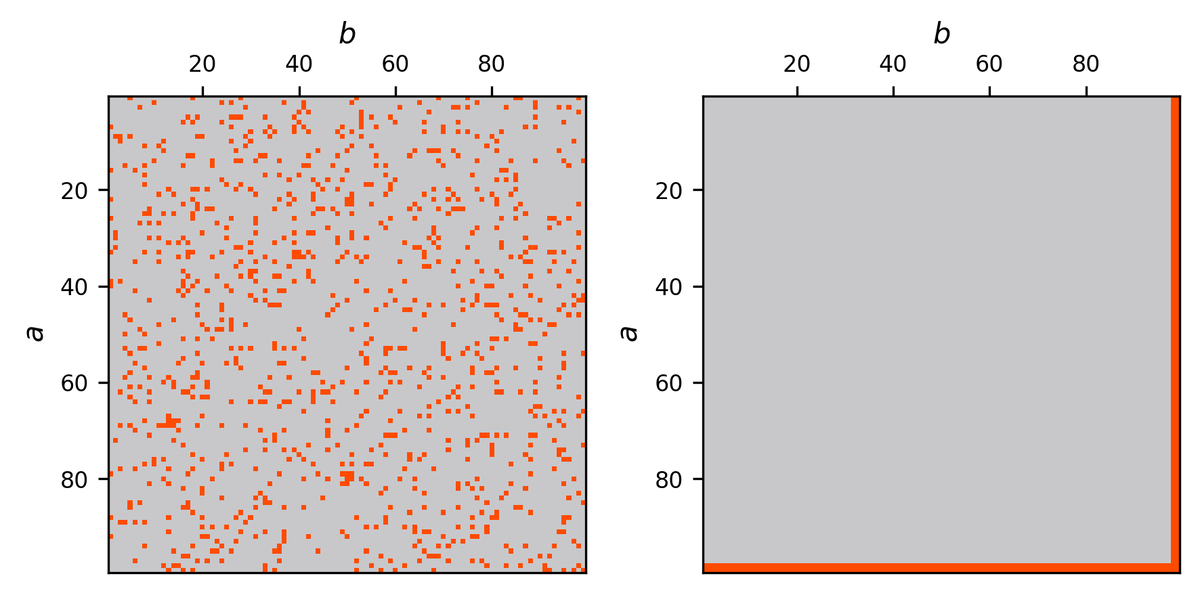
å·¦ã®ã‚ˆã†ãªãƒ©ãƒ³ãƒ€ãƒ ãªãƒ‘ターンã«ã¯ã€Œç©´ã€ãŒå¤šãã€ã‚¼ãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã¯ä¼¸ã³ã¾ã›ã‚“。å³ã®ã‚ˆã†ã«ç°¡å˜ãªå•é¡Œã‚’確実ã«æ£è§£ã—ã€ã‚µã‚¤ã‚ºãŒå¤§ããªé›£ã—ã„å•é¡Œã‚’ã€Œé †å½“ã«ã€é–“é•ãˆã‚‹ãƒ¢ãƒ‡ãƒ«ã¯ã‚¼ãƒã‚¨ãƒ©ãƒ¼å¢ƒç•ŒãŒå¤§ãããªã‚Šã¾ã™ã€‚åŒã˜æ£è§£çŽ‡ã§ã‚‚ã€å³ã®ã‚ˆã†ãªé–“é•ãˆæ–¹ã‚’ã™ã‚‹æ–¹ãŒæ‰±ã„ã‚„ã™ã好ã¾ã—ã„ã§ã™ã€‚æ£è§£çŽ‡ã§ã¯ã“ã®åŒºåˆ¥ã¯ã¤ãã¾ã›ã‚“ãŒã€ã‚¼ãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã§ã¯åŒºåˆ¥ãŒã¤ãã¾ã™ã€‚
例ãˆã° Qwen2.5-72B-Instruct ã® 1×1 ~ 99×99 ã®æ£è§£çŽ‡ã¯ 98.6% ã§ã™ã€‚ã‚‚ã—完全ã«ãƒ©ãƒ³ãƒ€ãƒ ã«ãƒŸã‚¹ã—ã¦ã„ã‚‹ã¨ã€ã‚¼ãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã¯ 10 未満ã«ãªã‚‹ã¯ãšã§ã™ã€‚1×1 ã‹ã‚‰ 10×10 ã¾ã§ã«ã¯ 100 å•ã‚ã‚‹ã®ã§ã€é–“é•ãˆã‚‹ç¢ºçŽ‡ãŒ 1.4% ã ã¨ã“ã®ç¯„囲㧠1.4 å•ç¨‹åº¦é–“é•ã†ã‹ã‚‰ã§ã™ã€‚ã—ã‹ã—ã€Qwen2.5-72B-Instruct ã®ã‚¼ãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã®å®Ÿæ¸¬å€¤ã¯ 42 ã§ã™ã€‚ã¤ã¾ã‚Šã€Qwen2.5-72B-Instruct ã¯ç°¡å˜ãªå•é¡Œã¯ç¢ºå®Ÿã«è§£ãã€é›£ã—ã„å•é¡Œã‚’ã‚ã‚‹ç¨‹åº¦ã€Œé †å½“ã«ã€é–“é•ãˆã¦ã„ã‚‹ã¨ã„ã†ã“ã¨ãŒåˆ†ã‹ã‚Šã¾ã™ã€‚ã“ã‚Œã¯æ£è§£çŽ‡ã¯ 98.6% ã®ä¸ã§ã‚‚ã€Qwen2.5-72B-Instruct ã¯å®Ÿç”¨ä¸Šæ‰±ã„ã‚„ã™ã„é–“é•ã„方をã™ã‚‹ã“ã¨ã‚’示ã—ã¦ã„ã¾ã™ã€‚
LLMのキモい算術 - ジョイジョイジョイ ã‚„ LLM のアテンションと外挿 - ジョイジョイジョイ ã§ç´¹ä»‹ã—ãŸã‚ˆã†ã«ã€LLM ã¯æ§˜ã€…ãªæ–¹æ³•ã§æŽ¨è«–å•é¡Œã‚’解ã„ã¦ã„ã‚‹ã“ã¨ãŒçŸ¥ã‚‰ã‚Œã¦ã„ã¾ã™ã€‚
æš—è¨˜ã‚„å …ç‰¢ã§ãªã„方法ã§å•é¡Œã‚’解ã„ã¦ã„ã‚‹ã¨ã€Œç©´ã€ã¯å¤šããªã‚Šã‚¼ãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã¯å°ã•ããªã‚‹ã§ã—ょã†ã€‚ゼãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã‚’大ããã™ã‚‹ã«ã¯ã€å …牢ãªã‚¢ãƒ«ã‚´ãƒªã‚ºãƒ やルールを身ã«ã¤ã‘ã‚‹å¿…è¦ãŒã‚ã‚Šã¾ã™ã€‚ゼãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã‚’評価指標ã¨ã—ã¦ç”¨ã„ã‚‹ã“ã¨ã§ã€åŒã˜æ£è§£çŽ‡ã®ä¸ã§ã‚‚ã“ã®ã‚ˆã†ãªå …牢ãªã‚¢ãƒ«ã‚´ãƒªã‚ºãƒ ã®ç²å¾—を促進ã§ãã‚‹ã¨è€ƒãˆã‚‰ã‚Œã¾ã™ã€‚
ã“ã®ã‚ˆã†ã«ã€ã‚¼ãƒã‚¨ãƒ©ãƒ¼å¢ƒç•Œã¯è©•ä¾¡æŒ‡æ¨™ã¨ã—ã¦æ£è§£çŽ‡ã«ã¯ãªã„好ã¾ã—ã„性質を複数もã¡ã€LLM ã®ä¿¡é ¼æ€§ã‚„ä¸å®‰å®šæ€§ã‚’評価ã™ã‚‹ä¸Šã§ä¾¿åˆ©ã§ã™ã€‚ãœã²ã€è‡ªç¤¾ã®ãƒ¢ãƒ‡ãƒ«ã®è©•ä¾¡ã‚’ã—ãŸã‚Šã€è‡ªåˆ†ã§ä½¿ã†ãƒ¢ãƒ‡ãƒ«ã®é¸å®šã«æ´»ç”¨ã—ã¦ã¿ã¦ãã ã•ã„ã。
ãŠã‚ã‚Šã«
SNS を眺ã‚ã¦ã„ã‚‹ã¨ã€ŒLLM ãŒã“ã‚“ãªã«ã™ã”ã„å•é¡Œã‚’解ã‘るよã†ã«ãªã£ãŸï¼ã€ã¨ã„ã†ãƒ‹ãƒ¥ãƒ¼ã‚¹ã¨ã€Œ LLM ã¯ã¾ã ã“ã‚“ãªã«æ„šã‹ãªé–“é•ã„ã‚’ã™ã‚‹ï¼ã€ã¨ã„ã†ãƒ‹ãƒ¥ãƒ¼ã‚¹ã§ã‚ãµã‚Œã¦ã„ã¾ã™ã€‚ã“ã®ã‚ˆã†ãªèƒ½åŠ›ã®ã‚®ãƒ£ãƒƒãƒ—ãŒéžå¸¸ã«å¤§ãã„ã“ã¨ãŒ LLM ã®æ‰±ã„ã¥ã‚‰ã•ã®è¦å› ã ã¨æ€ã„ã¾ã™ã€‚
ã“ã®ç ”究ã§ã¯ã“ã®ã†ã¡ã€Œ LLM ã¯ã¾ã ã“ã‚“ãªã«æ„šã‹ãªé–“é•ã„ã‚’ã™ã‚‹ï¼ã€ã®æ–¹å‘ã®ä¸»å¼µã‚’システマãƒãƒƒã‚¯ã«è¡Œã†æ–¹æ³•ã‚’æ•´ç†ã§ããŸã¨ã“ã‚ãŒæ°—ã«å…¥ã£ã¦ã„ã¾ã™ã€‚
GPT-5.2 を見ã¦ã„ã‚‹ã¨ã€ã¾ã 「穴ã€ã¯æ•°å¤šãã‚ã‚Šã€AI ã®å°»ã¬ãã„ã‚’ã™ã‚‹ä»•äº‹ã¯ã—ã°ã‚‰ã続ããã†ã«æ€ã„ã¾ã™ã€‚ã“ã®ç©´ãŒåŸ‹ã¾ã‚‹æ—¥ã¯ãã‚‹ã®ã§ã—ょã†ã‹ã€‚皆ã•ã‚“も考ãˆã¦ã¿ã¦ã„ãŸã ã‘ã‚Œã°å¹¸ã„ã§ã™ã€‚
è‘—è€…æƒ…å ±
ã“ã®è¨˜äº‹ãŒãŸã‚ã«ãªã£ãŸãƒ»é¢ç™½ã‹ã£ãŸã¨æ€ã£ãŸæ–¹ã¯ SNS ãªã©ã§æ„Ÿæƒ³ã„ãŸã ã‘ã‚‹ã¨å¬‰ã—ã„ã§ã™ã€‚
æ–°ç€è¨˜äº‹ã‚„スライド㯠@joisino_ (Twitter) ã«ã¦ç™ºä¿¡ã—ã¦ã„ã¾ã™ã€‚ãœã²ãƒ•ã‚©ãƒãƒ¼ã—ã¦ãã ã•ã„ã。
ä½è—¤ 竜馬(ã•ã¨ã† りょã†ã¾ï¼‰
京都大å¦æƒ…å ±å¦ç ”究科åšå£«èª²ç¨‹ä¿®äº†ã€‚åšå£«ï¼ˆæƒ…å ±å¦ï¼‰ã€‚ç¾åœ¨ã€å›½ç«‹æƒ…å ±å¦ç ”究所助教。著書ã«ã€Žæ·±å±¤ãƒ‹ãƒ¥ãƒ¼ãƒ©ãƒ«ãƒãƒƒãƒˆãƒ¯ãƒ¼ã‚¯ã®é«˜é€ŸåŒ–ã€ã€Žã‚°ãƒ©ãƒ•ãƒ‹ãƒ¥ãƒ¼ãƒ©ãƒ«ãƒãƒƒãƒˆãƒ¯ãƒ¼ã‚¯ã€ã€Žæœ€é©è¼¸é€ã®ç†è«–ã¨ã‚¢ãƒ«ã‚´ãƒªã‚ºãƒ ã€ãŒã‚る。