交錯 (幾何)
(重定向自交错)
在幾何學中,交錯是一種將多邊形、多面體、密鋪、鑲嵌或更高維的多胞體交替地去除頂點的一種多面體變換[1] 。考克斯特符號將交錯變換記為h。
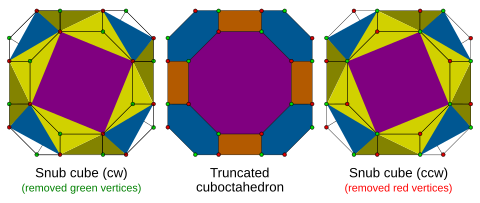
紅色與綠色標示出了兩種可進行交替的頂點。 透過交替變換,移除大斜方截半立方體的頂點之後,形成了扭稜立方體,其原先的八邊形變為正方形,其中一個是逆時針旋轉、另一個順時針旋轉
由於交錯變換會導致每個面的頂點數都減少一半,因此此種變換只適用於每個面的邊樹是偶數個的多面體。另外若作用於四邊形面上,則導致四邊形退化變成二角形,通常變成只剩一條邊。
半變換
编辑半變換(英語:half)是交錯變換的一種,即交錯的把多面體一半的頂點全部去除,不留下任何與該頂點相連的邊和面,並且於剩餘的頂點建立新的面。如:正方體經過此種變換會變成正四面體。
| → |
此種變換會造成面數變為原本面數再加頂點數的一半、頂點數變為原來的一半而邊數不變。若原本有正方形面會造成面數只剩下頂點數的一半。
抽象半變換
编辑抽象半變換(英語:hemi)是另一種半變換,也是去除該多面體一半的頂點,但是不是交錯,也不建立新的頂點、邊和面,而是將舊的頂點直接互相共用。此種變換會產生抽象多面體。此種變換會造成面數、頂點數與邊數都變成原來的一半。
四分之一變換
编辑四分之一變換是進行兩次半變換。
扭稜
编辑扭稜是交錯進行截邊的一種變換。
交錯截角
编辑交錯截角是交錯進行截角的一種變換。
| 名稱 | 原本 | 交錯截角 | 截角 |
|---|---|---|---|
| 正方體 截半四面體的對偶 |
交錯截角立方體 倒角四面體 |
截角立方體 | |
| 菱形十二面體 截半立方體的對偶 |
交錯截角菱形十二面體 倒角立方體 |
截角菱形十二面體 | |
| 菱形三十面體 截半二十面體的對偶 |
交錯截角菱形三十面體 倒角二十面體 |
截角菱形三十面體 | |
| 三角化四面體 截角四面體的對偶 |
交錯截角三角化四面體 倒角截角四面體 |
截角三角化四面體 | |
| 三角化八面體 截角立方體的對偶 |
交錯截角三角化八面體 倒角截角立方體 |
||
| 三角化二十面體 截角十二面體的對偶 |
交錯截角三角化二十面體 倒角截角十二面體 |
參考文獻
编辑- ^ Coxeter, Regular polytopes, pp. 154–156 8.6 Partial truncation, or alternation
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- 埃里克·韦斯坦因. Snubification. MathWorld.
- Richard Klitzing, Snubs, alternated facetings, and Stott-Coxeter-Dynkin diagrams, Symmetry: Culture and Science, Vol. 21, No.4, 329-344, (2010) [1](页面存档备份,存于互联网档案馆)
外部連結
编辑- Olshevsky, George, Alternation at Glossary for Hyperspace.
- Polyhedra Names, snub (页面存档备份,存于互联网档案馆)
| 原像 | 截角 | 截半 | 過截角 | 對偶 | 擴展 | 全截 | 交錯 | ||
|---|---|---|---|---|---|---|---|---|---|
| 半變換(章節) | 扭稜 | ||||||||
| t0{p,q} {p,q} |
t01{p,q} t{p,q} |
t1{p,q} r{p,q} |
t12{p,q} 2t{p,q} |
t2{p,q} 2r{p,q} |
t02{p,q} rr{p,q} |
t012{p,q} tr{p,q} |
ht0{p,q} h{q,p} |
ht12{p,q} s{q,p} |
ht012{p,q} sr{p,q} |