An Enumerative Geometry for Magic and Magilatin Labellings

Abstract.

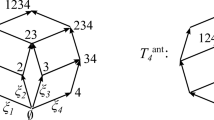
A magic labelling of a set system is a labelling of its points by distinct positive integers so that every set of the system has the same sum, the magic sum. Examples are magic squares (the sets are the rows, columns, and diagonals) and semimagic squares (the same, but without the diagonals). A magilatin labelling is like a magic labelling but the values need be distinct only within each set. We show that the number of n  ×  n magic or magilatin labellings is a quasipolynomial function of the magic sum, and also of an upper bound on the entries in the square. Our results differ from previous ones because we require that the entries in the square all be different from each other, and because we derive our results not by ad hoc reasoning but from a general theory of counting lattice points in rational inside-out polytopes. We also generalize from set systems to rational linear forms.